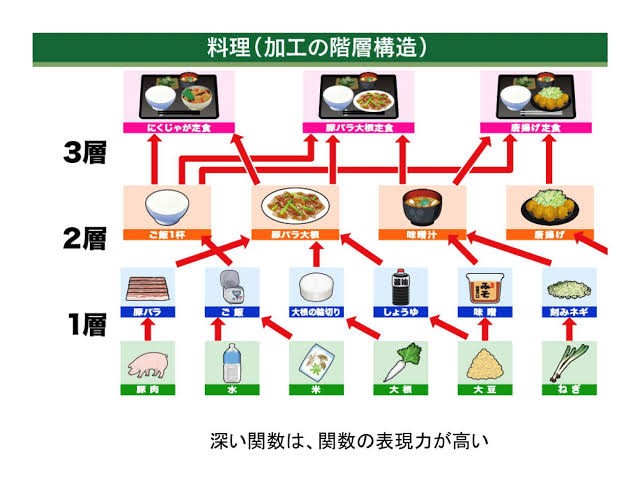
Table of Contents
この文章は何か
自分が会社で毎年ボランティアでやってる機械学習の授業です。【参加方法】何らかの方法で私に課題を解いて送ってオンライン授業 / 私の会社(株式会社フェズ)でバイトするなど
勉強会の目的・レベル感
最終ゴールは、SOTAの論文をバリバリ読めて実装できるようになることです。
“Markov Chain Monte Carlo”
そのためにまず最も大事な機械学習であるMCMCができるようになること。さらに、MCMCの数理を微分とエントロピーで説明できるようになること。その先にHintonのDeep Learning研究があります。
1948年から2012年までを駆け抜けます。
学部3年生レベル・初学者向けです。
教科書
故Mackay教授の手になる無料の教科書です。最新情報も載ってる上位互換版は探し中です。
この本のいいところは真の意味で機械学習がわかるところです。
各社・研究室独自教材を出してますので、続編は違う本でやるかもしれません。
無料版pdf(公式)リンク
Amazon(紙版)へのリンク

各回に必須課題をつけています。私に聞いてくれればいつでも添削・解説します。
【入学式】
まず全体のペース配分を決めます。
各Partにかける時間ですが、急いで読むなら1日ずつ、ゆっくりやるなら1ヶ月ずつで、それ以上はだれます。
- Part1(1~6) ベイズの定理とエントロピー
- Part2(7~12)クラスタリング
- Part3(13~16)MCMCとボルツマンマシン
- Part4(17~20)NNとRBM
第1回 スターリングの公式
それでは、スタートです。
機械学習で最も多用される数学、それは対数(log)です。
logが多用される理由のひとつは、コンピューターで計算を行うために、桁数に限界があることです。もうひとつは、積を和に変換できることです。
機械学習では大量のデータを学習します。この最も単純な場合は、独立試行列です。
独立試行列の計算には階乗n!が多用されます。階乗計算を簡単にしてくれるのが、スターリングの公式です。
Point
以下の3つは、全て同じことを意味しています。
- ドモアブルラプラスの定理
- スターリングの公式
- 二項係数がバイナリーエントロピー関数Hを使ってlog NCr=NHと書けること
応用編として、マクミランの定理の説明もします。
1 100!の桁数を求めよ。
2 二項分布がポアソン分布で近似できる十分条件を答えよ。上の問題を応用して、λ!の近似を考えよ。
エントロピーとはE[logp]のことです。
3 エントロピーとlogNCrはrがいくつの時に等価になるでしょうか。
4 エントロピーは機械学習の核心的な概念です。大数の法則により、エントロピーがほぼ定数になることを証明してください。(ヒント:エントロピーの分散を計算してみてください。)
課題1
第2回 Noisy Channel
機械学習の結果、元のデータを再現できる割合を、精度accuracyと言います。この精度が100%になる場合はほぼありませんから、機械学習においてはデータはある意味劣化していると考えられます。
この劣化現象について考察するために、まずは、noisy channelにおける冗長コーディングを学びましょう。冗長コーディングは、生物が個体情報をDNAに保存するときにも使われています。
ここでは、画像を劣化させて復元する問題を、確率的推論で解きます。
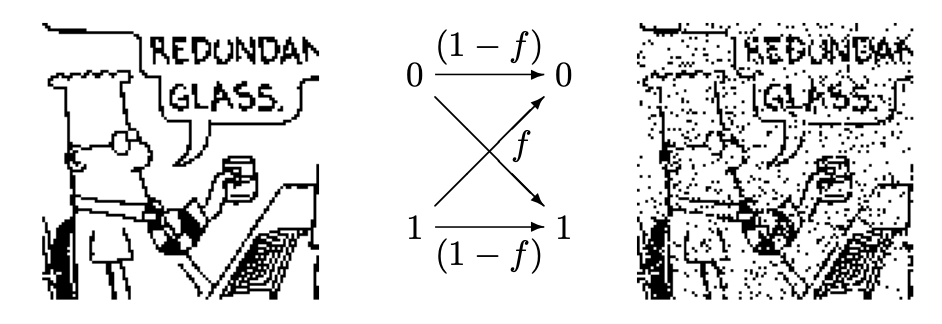
この劣化の際に失われた情報を、エントロピーとして測ることが出来ます。
1 Excersize 1.2。(ヒント:問題文を条件付き確率で表す)
2 60台のノイズだらけのハードディスクを使えば、1台の精度が高いハードディスクを作れます。その方法を説明してください。
3 Excersize 1.3。(ヒント:二項分布とスターリンの公式)
4 Encoder/Decoderを使った機械学習のモデルを1個説明してください。(ヒント:オートエンコーダー)
課題2
ヒント:
最後に、自然言語のエントロピーが語られます。
第3回 ベイズの定理
前回、冗長コードのdecodingに使われたのが、ベイズの定理Bayes Theoremです。
ベイズの定理は式の形や計算結果が直感に反するため、多くの人が覚えにくいと感じるようです。でも、習うより慣れろです。覚えるまで100回使えば大丈夫。100回使って覚えられなかったひとはいません。
右辺のP(x|θ)を反転して左辺のP(θ|x)にする道具、と捉えていろいろな問題でベイズの定理の正しさを確認し、体に覚え込ませる回です。
「近所の人がスティーブのことを次のように描写しました。『スティーブはとても内気で引っ込み思案だ。いつも頼りにはなるが、基本的に他人には関心がなく、現実の世界にも興味がないらしい。物静かで優しく、秩序や整理整頓を好み、細かいことにこだわる。』さてスティーブは図書館司書でしょうか、それとも農家の人でしょうか?」
課題3
第4回 エビデンス
ベイズの定理は、右辺のP(x|θ)を反転して左辺のP(θ|x)にする道具です。
この両辺はパラメーターの関数であって、データは定数であることに注意しましょう。右辺のP(x|θ)は、xの関数ではなく、xは定数で、θの関数なのです。
Never say ‘the likelihood of the data’. Always say ‘the likelihood of the parameters’. The likelihood function is not a probability distribution.
p29
一方、ベイズの定理の分母P(x)は、データxのEvidenceと言います。
物理では分配関数というやつです。モデル比較で使います。
とはいえ、エビデンスは積分を含みますから、計算は簡単ではありません。ここでは、積分が簡単なベータ関数とガンマ関数を使った例で、エビデンス比較の方法を学びます。
課題:【ベントコイン】
曲がったコインがあって、確率pで表が出ますが、その確率はわかりません。たくさん投げて、推定する必要があります。
100回投げたら、表が40回、裏が60回でした。
1 ベータ分布B(1,1)を事前分布としてpを求めよ。
2 ベータ分布B(10,10)を事前分布としてpを求めよ。
3 ベータ分布B(100,100)を事前分布としてpを求めよ。
課題4
第5回 エントロピー
さて、今回ついにこの教科書の中核概念であるエントロピーが登場します。
前回、データxのエビデンスを扱いました。データxのエントロピーも重要です。
エビデンスは確率であり、エントロピーは情報量の期待値(ビット)であることに注意してください。別物です。
共通点は、両方がデータがもつ情報量の大きさを表していることです。エビデンスは生成確率の低さでデータのレア度=シャノン情報量の合計を表し、エントロピーは分布Pに従う独立試行列データの平均情報量=シャノン情報量の平均を表します。
さて、難しい話になりましたが、分布PとQに対して計算される、相対エントロピー=Kullback Leibler Divergenceについても学びます。
KLDは確率分布空間内における、PとQとの間の擬距離です。なぜ距離とエントロピーが結びつくのかというと、両方フィッシャー計量の積分だからです。
KLDは常に正です。このJensenの不等式も重要です。
これをちゃんと理解すれば過学習判定に使うAICを計算することもできます。
1 Table2.9を見て、アルファベットの1文字ごとのシャノン情報量を確認せよ。qの情報量はeの情報量の3倍であるが、これは何を意味するか(答え:eの頻度がqの頻度の8倍であることを意味する)
2 Example2.12 アルファベットの平均情報量は4.11ビットである。これは、5ビットあれば32通りあるから、26通りのアルファベットが区別できることを意味している。これを説明せよ。
3 式(2.39)が独立な確率変数同士にしか成り立たない理由を説明せよ。
4 Example2.13 アルファベットと数字の36通りだが4.95ビット(32通り相当)しかないのはなぜか説明せよ。
課題5
第6回 モデル選択
さてここまでで学んだ機械学習とは、
「データをよく再現できる学習モデルP(x|θ)を選び、そのパラメーターθの事後分布P(θ|x)を求めること」
だと言えるでしょう。よく知られているニューラルネットワークや決定木でもこの基準は使えます。
モデルの選択肢は無数にあります。どうやってモデルに優劣をつけ、無数のモデルの中から最良のモデルを選び出せばいいのでしょうか。(モデル選択の問題)
まずはベイズモデル同士の優劣判定法について学びましょう。これにもいくつか方法はあるのですが、まずは最も単純な方法を学びます。
エビデンスを使ってモデル比較を行います。選択したモデルを「仮説」といいHで表します。
エビデンスP(x)をP(x|H)と書くと、実はこれは単なるデータの生成確率ではなく、仮説に対する証拠Evidence・信念Belief=事前分布から計算した尤度であることがわかります。
例えば0と1のシーケンスを説明するために、ベントコインを持ってくることも6面サイコロを持ってくることもできます。しかしコインのほうが適しています。なぜなら尤度が圧倒的に大きいからです。これがエビデンスベースのモデル比較です。
この方法はモデルの優劣がデータが増えるほど明らかになるという現象を折れ線グラフで可視化できます📈
うっかり感動してしまいますが、この時点では、過学習を可視化できていないという欠点があります。これについてはのちの章で学習します。
殺人事件の現場に、被害者のものではない2つの血痕があり、O型とAB型でした。
オリバーの血液型はO型でした。この血痕があったことにより、不運なオリバーは重要参考人として裁判にかけられました。オリバーは有罪でしょうか?
(答え:血痕があったことでオリバーが無罪である確率が高まります。これをエビデンスベースモデル比較で説明してください。)
(ヒント:O型は人口の60%、AB型は人口の1%です。)
課題6
【前期中間試験】
さて、ここまでは理解できましたでしょうか?
1つでもできなかったら最初からやり直しです!
1. 「機械学習とは一様分布による近似である」をマクミランの定理を使って説明せよ
2. 「エンコード・デコード」の概念を説明せよ
3. 「ベイズの定理」を説明せよ
4. 「ガンマ関数とベータ関数を使ったベイズ推定」をコイン投げ問題を使って説明せよ
5. 「機械学習できたときに成り立つ式KLD=0を説明せよ。(十分条件)」
中間試験1
第7回 ティピカリティ
第5回で、確率変数のエントロピーを測りました。これを使って、「実験で得られた情報量」をビットで計測する方法を学びます。
実験を繰り返す場合、毎回得られる情報量を合計すると、独立試行列全体の情報量が得られます。これを、エントロピーの相加性(<示量性)と言います。
実験データ列を文字列と考えて任意のアルゴリズムで圧縮します。シャノンの定理から導かれるデータ圧縮の最大効率は、独立試行列に従うと仮定して計算したエントロピー(平均シャノン情報量)に一致します。
シャノンの情報源符号化定理は、実験回数Nを増やすことでこの平均情報量が正確に最大効率に近づくことを表しています。
ところが、もうひとつ不思議なことが起こっていることにも気を付ける必要があります。
実は、実験回数Nをどんなに増やしても、全てのデータは、典型領域Typicalityにしか生成されないのです。
高次元空間を眺めるとき、直感に反することがよく起こります。このティピカリティは重要な例で、データ点が実は高次元球面上にしか分布していないことを説明します。原点の周りは常にスカスカなのです。
このティピカリティ領域を当てることこそが機械学習なのです。
12個の鉄球があります。11個は同じ重さで、1つだけ重さが違うのがあります。軽いか重いかはわかりません。
2つの皿がついた天秤を使って、この1つを見つけ、それが他の球より重いのか軽いのかを当ててください。
天秤を使う回数を最小にするにはどうしたら良いでしょうか?
あなたのすべての行動のエントロピーを逐一計算しながら行動してください。
課題7
最後に、漸近等分配性Asymptotic Equipartition、別名マクミランの定理により、独立試行列は典型領域の定義関数上にほぼ一様分布することを学びます。
第8回 総当たり法
※難解な200ページを飛ばすため、ここでp89から一気にp293に移動します。
今まで学んだ機械学習を総当たりbrute forceで実行してみます。
以下の問題、機械学習など使うまでもなく、人間の常識と直感だけでも答えられそうですが、どうでしょうか。
課題:【警報機】
フレッドはロサンジェルス在住で、家から100キロ離れた会社に通っています。
仕事中に、彼に近所の人から電話がかかってきて、フレッドの家の警報機がなっていると教えてくれました。
この時点で、フレッドの家に泥棒が入った確率は何%でしょうか?
不安になってフレッドは家に帰ることにしました。車の中で、ラジオが、今日フレッドの家の近くで小さな地震があったことを告げました。
『Oh』彼は安心してつぶやきました。『きっと泥棒じゃなくて、地震のせいで警報機が誤作動したんだな。』
この時点で、フレッドの家に泥棒が入った確率は何%でしょうか?
課題8-1
これをベイズ推定で解くことで、『常識的』な結果を数値化します。(Augmented Common Sense)
第5回のエントロピーを使って、「実験で得られた情報量」をビットで計測できることがわかりましたから、電話とラジオそれぞれについて情報量が数値的に求められるわけです。
これはパラメータ空間が離散的な簡単な例ですが、brute forceだと膨大な計算が必要になることがわかります。
次に、パラメータ空間が連続的だと、Gridをbrute forceするだけで天文学的な計算が必要になり、宇宙の寿命よりも長い時間がかかることを混合ガウシアンを例に学びます。
10個の正規分布からなる混合正規分布をGrid Searchする場合の計算量を見積もれ。
課題8-2
第9回 Hard K-meansとSoft K-means
前回の混合ガウシアンによるフィッティングを、brute forceではなく簡単に学習する方法があります。AssignmentとUpdateという作業を機械的に繰り返すK-meansアルゴリズムです。
Assignment Step
Update Step
Soft K-meansという、「逆温度β」をハイパーパラメーターにもつモデルも学習します。(僕が一番好きなアルゴリズムです。)
二つの正規分布が、ほとんど重なっている状況を考えます。
μ=-1, σ=1と、μ=+1, σ=1のような状況です。
Hard K-meansで得られる解とSoft K-meansで得られる解は全然違います。これを説明してください。
課題9-1
実は、混合ガウシアンによるフィッティングをNeuton Raphson法でMaximum Likelihoodで解くとSoft K-meansが得られます。そして、Soft K-meansにおいてβ=∞の極限を取るとNeuton Raphson法はHard K-meansのAssigment/Updateの式に一致します。
1 なぜ一次微分∂L/∂μを足すか考えよ。
2 なぜ二次微分∂^2L/∂μ^2で補正するか考えよ。
3 β=∞の極限をとれ。
課題9-2
第10回 Maximum Likelihoodの過学習
初めて、過学習について学びます。
実は、Soft K-meansはKを過剰にすると盛大に過学習してしまうのです。
具体的には、K=N(データの個数)にすると、全てのデータ点が重心と予測され、尤度は無限大に発散します。
この解決策は、Maximum LikelihoodではなくMaximum a posterioriを使うことです。
課題:【星を見る男】
二人の男が鉄格子のはまった窓から外を見ていた。一人は星を見ていた。もう一人は窓のサイズをベイズ推定しようとしていた。
あなたには座標{(x,y)}の組みが与えられる。また、窓の淵は暗すぎ、星からも十分離れているため全く見えない。 窓は長方形であり、星の位置はランダムかつ独立である。まずは次の例を使う。
例) “北斗七星” (7,7), (8,6), (9,7), (9,8), (11,9), (13,10), (14,9)
1. maximum likelihoodを使って、窓の4点の座標を求めよ。likelihoodの式も提出せよ。
2. 上記モデルを壊すようなデータを考え、ablationを行え。
課題10
第11回 Laplace法
最後に、あらゆるデータに対して使えるラプラス近似を学びます。
二階微分が存在する関数は二次までのテイラー展開ができます。
この事実を使って、ほとんど全ての多次元確率分布を多次元正規分布で近似できます。
課題:【ベイズ回帰】
Exercise 27.3
N個のデータ点{(x_n, t_n)}をラプラス法で近似すると、回帰残差(residual)が正規分布に従うモデルになる。
t ~ Normal(a+bx, σ^2)
1 aとbの事前分布を正規分布にして、事後分布を求めよ
2 事後分布をラプラス法で近似せよ
3 近似事後分布で、x_{N+1}が与えられた時予測値を答えよ。
課題11
第12回 Occum Factor
モデル比較は第6回にやりましたが、離散モデル同士の比較でした。
ここでは、連続モデル同士の比較を行います。
特に、シンプルなモデルと、複雑なモデルで、シンプルなモデルが選好される理由が、自然科学の「オッカムの剃刀」の定量版であることを説明します。
Excercise 28.2
H1: y = b + ε P(b) = P(ε) = Normal(0, 1)
H2: y = ax + b + ε P(b) = P(ε) = P(a) = Normal(0, 1)
の2つのモデルを比較する。Dataset={(-8, 8), (-2, 10), (6,11)}のEvidence of Data=P(D | H1), P(D | H2)を求めよ。
次に、Evidence Ratio of Model=P(H1 | D) / P(H2 | D)を求め、どちらのモデルが優れているか結論せよ。
課題16
P(D | H1) = 3 * 10^(-64)
P(D | H2) = ? * 10^(-36)
P(H1 | D) / P(H2 | D) = 10^(+28)
【前期期末試験】
ここまでで使える機械学習は、Bayesian NetworkとK-meansとBayesian Regressionのみです。
なぜ、このような構成になってるのでしょうか?
この3つのモデルは全て正規分布しか使わないモデルなのです。ですので、まずは正規分布だけでどれだけ多くのことができるか学んだということなのですね。
正規分布以外の分布は、この次の章の§23(311ページ目)で初めて出てくるのです。
機械学習が成功するためには、いい特徴量が抽出されている必要がある。
1 データのエントロピーと、特徴量のエントロピーの違いを説明せよ。
2 Bayesian Networkで、データのエントロピーを抽出する方法を説明せよ。
3 K-meansで作ったクラスタのエントロピーは、データのエントロピーに比べどうなっているか説明せよ。
4 Bayesian Regressionが、データに対してエントロピー最大のモデルであることを説明せよ。
前期卒業試験
第13回 モンテカルロ積分
ベイズ推定における「SGD」それがサンプリングです。
MCMCが万能なので、それを理解することが目的となります。
ここでは、MCMCの一種であるメトロポリス・ヘイスティング法を理解しますが、3段階を追って理解します。
- Importance Sampling
- Rejection Sampling
- 2つを合わせたMetropolis Hastings Method
ボックス・ミュラー法を実装し、Normal(a,b)に従う乱数を10000個生成し、ヒストグラムを描いて確かめよ。
課題17
第14回 MCMC
機械学習史上最大の発明、MCMC(マルコフチェーン・モンテカルロ)。
メトロポリス・ヘイスティングス法は、MCMCの一種である。
acceptance ratioが、マルコフチェーンにおける詳細釣り合いの式と一致することを確認せよ。
課題18
第15回 ギブスサンプリング
周辺化して1次元ずつサンプリングしていく方法。直角にしか動けないMCMC。
MCMC ⊃ Metropolis Hastings ⊃ Gibbs であることを確認せよ。
Gibbsサンプリングが失敗するケースを考えよ。
課題19
第16回 イジング・ホップフィールド・ボルツマン
磁石のモデルだが、機械学習によく転用される。ホップフィールドネットワーク・ボルツマンマシンの簡単化した場合がイジングモデル。
ヒントン(1986)が有名にした。
ボルツマンマシンはディープラーニング前に通っておくべき洗礼
イジングモデルはxがバイナリ(スピン)
ホップフィールドネットワークはHがiに依存(外場)
ボルツマンマシンはxが連続値
いずれも全く同じくギブズサンプリングで学習出来る。
【後期中間試験】
サンプリング系の問題にする予定
第17回 ニューロン
理論的にはニューロンはベイズ回帰の延長線上にあります。
その場合、
- Activation = tanh(≠ReLU)
- Loss function = cross Entropy(≠softmax)
- Regularization = L2
となります。cross Entropyが+∞のペナルティを持つことに注意してください。
学習方法として、Gradient Descent / Stochastic Gradient Descent / Gibbs Samplingがあることを学びます。
学習方法がなんであれ、学習結果が2^N通りの関数しかないということを学びます。そのため、データ点が少なければ、ニューロンは必ず学習可能です。(過学習の可能性は排除できません)
では限界データ点個数は幾つなのでしょうか。それは、モデルのVapnik–Chervonenkis (VC) 次元と呼ばれる数になります。
第18回 多層ニューラルネットワーク
多層ニューラルネットワークによって、任意の関数をフィッティングすることができます。任意の関数をフィッティングするには、
- 非線型関数の導入
- 隠れ層の個数を増やす
- ディープにする=隠れ層の数を増やす
学習困難性の問題と、過学習の問題があります。
学習困難性
隠れ層を持つネットワークは必然的に2層以上になり、バックプロパゲーションがないとうまくトレーニングできない。具体的には、計算時間が遅く、Loss関数が収束しなくなってしまう。
過学習
隠れ層を持つネットワークはパラメーター数が多すぎ、過少なデータに対して過剰適合する可能性がある。
ヒントン
バックプロパゲーションを有名にした。RBMへの適用(CD法)が有名。
第19回 潜在変数
ベイズの最強兵器、階層ベイズ=グラフィカルモデル
第20回 制限ボルツマンマシン・ディープラーニング
43章2節「Restricted Boltzmann Machine(2006)」を読みます。
伝説の論文を読みます。
この論文によりpretrainが生まれました。
そして2012年にAlexnetがHinton研から生まれました。
これを表す図を、松尾豊研究室に敬意を表し、卒業証書として進呈したいと思います。