Table of Contents
コンピューター発明前…
1976年、Apple Computerは、Apple Iという最初のパーソナルコンピューター50台を出荷した。
それに先立つこと50年前 – 1926年、シュレディンガーはシュレディンガー方程式を含む、量子力学についての一連の論文を発表した。コンピューターは電気で動き、0と1のデジタル情報を処理する。しかしこの方程式がなければ、人類は未だに、「なぜ金属には電流が流れるのか」という基本的な問いにさえ、答えられなかっただろう。
シュレディンガー方程式は、無限次元の複素数ベクトルに対する方程式である。
ψ(プサイ)は無限個の複素数からなるベクトル、(∂/∂x)^2は無限×無限の複素数行列なので、数学的には簡単な微分方程式だ。重要なのはψの意味である。
ψは波動関数もしくは量子状態ベクトルと呼ばれる。波動関数という名前は、電子を含むあらゆる粒子は波であるという事実を意味する。状態ベクトルという名前は、考える量子的対象=電子の状態である。例えば鉄球であれば重心と重心速度の分の3+3=6個の実数で状態を表現できるが、電子は複雑なものなので、状態の描写には無限個の「複素数」が必要なのだ。そんな複雑なものが、金属の中を流れているのだ。
面白いのは、無限の有限倍は無限なので、電子や陽子の有限個の集合体である人体も無限次元ベクトル1個の方程式であるシュレディンガー方程式で表すことができることだが、それはまた別の機会にしよう。
シュレディンガー方程式は、状態を表す無限次元のベクトルが刻々と変化することを表している(d/dt)。これが「電子が金属の中を流れる」ということだ。この式はより一般的かつ簡単に式変形もできて、ハミルトン・ヤコビ方程式という。
ハミルトン・ヤコビ方程式からシュレディンガー方程式を再現することができる。
よってハミルトン・ヤコビ方程式のSは物質波の「位相」であり、更に変動スケールがプランク定数サイズであることがわかる。このことは、物質波がプランク定数サイズの波長で振動する複素数波であることを表している。時間発展ルールであるハミルトニアンの形を変えれば、物質波を表す状態ベクトルが電子になったり陽子になったりする。
電子の状態ベクトルを図示してみよう。例えば水素原子の電子雲を図示してみると次のようになる。
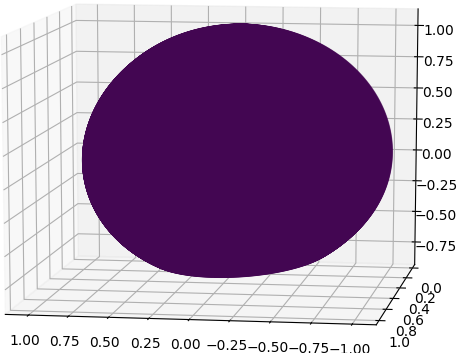
これは専門的になるが、主量子数n=1・方位量子数l=0に対応する1s軌道である。3次元の波を図示するのは不可能なので、波の振幅を2次元球面断面上で色で可視化した。これは最も単純な軌道なので、球面上では定数関数ということである。直径方向には動径関数に従って減衰してゆく。
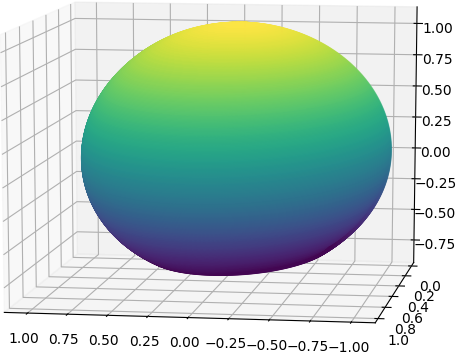
これは、主量子数n=2・方位量子数l=1に対応する2p軌道である。p軌道には直線的な方向性があり、xyzに対して3通りのp軌道が存在する。
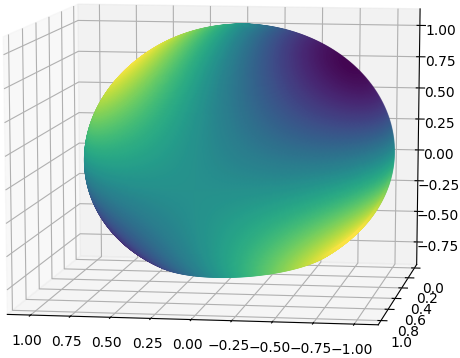
最後に、主量子数n=3・方位量子数l=2に対応する3d軌道を図示した。d軌道には十字型の紋章が現れることがわかる。
ここまでのまとめ
1926年に、電子のことがわかり始めた。コンピューターの発明まであと50年。
Q&A: 無限個の複素数とは
A: 電子の状態を表すことは、波の形を表すことに近いです。波の形は無限個のフーリエ係数で表されます。波の形は有限個の数では表現できないのです。電子はもっと複雑なので無限個の複素数です。
Q&A: 電子雲と状態ベクトル
A: 電子雲の形から状態ベクトルを計算する方法を説明します。球面調和関数全ての集合はそれぞれを基底とした無限次元ベクトル空間になるので、それに複素数係数をかけたものが状態ベクトルです。これはフーリエ変換に近いです。
逆に状態ベクトルから電子雲の形を計算する方法を説明します。状態ベクトルを逆フーリエ変換してそれぞれの球面調和関数を重ね書きしたものが電子雲の形になります。
Q&A: 電子雲を書くプログラム
A: 水素原子オンリーですが、こちらになります。
https://github.com/TheBigComputing/TheBigComputing/blob/master/1_quantum/Spherical.ipynb
その他のQ&Aも、コメントをつけていただけたら出来るだけお答えします。
理解度確認
- S波をつくるプログラムをかけるか
- 水素原子のS波を表す状態ベクトルがわかるか
- 「電子が金属を流れる」という現象はシュレディンガー方程式とどう関係あるのか説明できるか