Table of Contents
何が問題なのか
どうでもいいことが気になって仕方ない。
LSTMは宇宙の真理を表しているのは周知の事実だが、果たしてsin波を学習することは出来るのだろうか。出来るに決まってるだろうって?いやいや、それは誤解だ。Seq2Seqのように時間自由度を十分持っていれば当然出来るよ。でもそれはLSTMと呼ぶには複雑すぎるモデルだ。
なのでもうちょっと正確に問題を提起しよう。LSTMには限られた個数(8個)のパラメーターしかないが、それが表現できる非線形性は、どれほどの自由度があるのだろうか。LSTMは過去のhiddenレイヤー(cell)のパラメーターを持つので周期2で振動させることは難しくないはずだ。では、どんな周期運動でも学習できるのだろうか。
そのようなことを一応考えて(?)、「sinカーブを再現出来るのか」という問題にアタックしてみようと考えた。
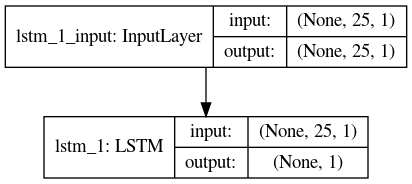
ネットワークがシンプルであることがわかる。また、パラメーターが8個であることは理論()と、以下のように出力確認した。
- h_t(隠れ状態)はoutput gateとc_t(セル)から自動的に決まるのでパラメータ0個。
- c_t(セル)はforget gate, c_(t-1)で忘却量が決まり、パラメータ0個。プラス、input gate, input, h_(t-1)(前回の隠れ状態)で入力量が決まるが、inputとh_(t-1)の線型結合を行うため、α*input + β*hなのでパラメータ2個。
- 3種類のゲートについては、いずれもinputとcellの線型結合を行うため、γ*input + δ*c_(t-1)なのでパラメータ2個。ゆえに
- forget gate → パラメータ2個。
- output gate → パラメータ2個。
- input gate → パラメータ2個。
なので合計8個である。

activationをNoneにする
sin波は非線形関数なので、できるだけ非線形性を系から除去したいと考えた。
recurrent_activationはsignoidにする
recurrent_activationはLSTM内部のループを表しているのだから、LSTM自体の非線形性なので除去すべきではないと考えた。tanhでもよさそうではある。
bias=0にする
sinカーブが平均値0なので。
失敗(1回目)
一見sinカーブを学習しているように見えて、実は学習できていない。おわかりだろうか。
よく見ると、前回の値をそのまま出力しているだけである。
sinを「遅く」しすぎると、単に前回の値を出力することでlossが下がってしまうのである。それともepoch=1000だから過学習なのか?
どうする?
- epochを下げる → いや、ゴールが間違っているのだからこの選択肢はだめだろう。
- 周期を変える
成功(1回目)
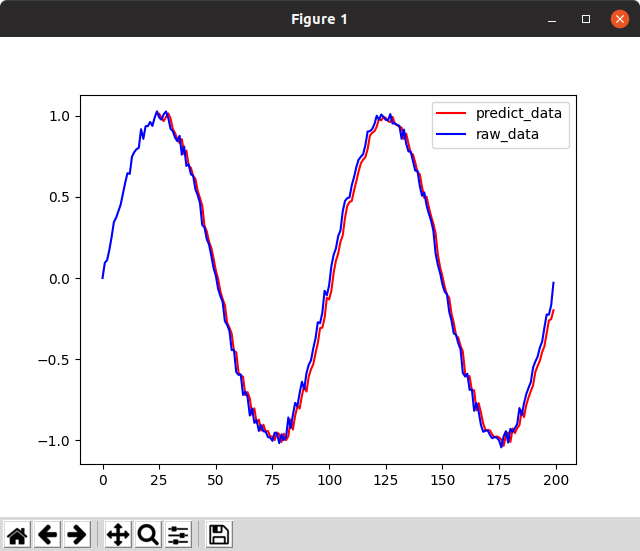
周期を1/4倍にしてみたので見てほしい。
さらにepochを進めてみよう。
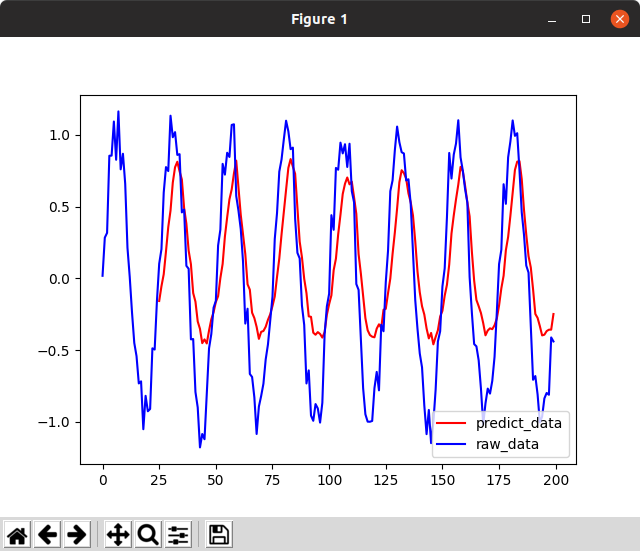
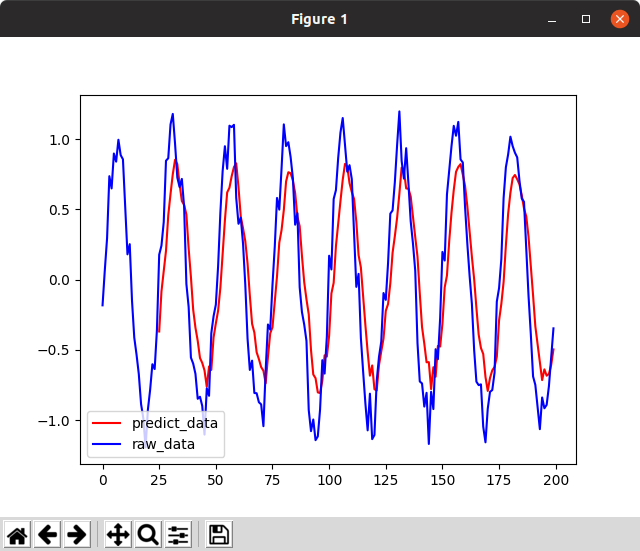
うーん、素晴らしい。前回と異なり「直前の値を出す」を学習していないという根拠は次の通り。
- 周期を1/fにすると、sin(ft)の微分はf倍になるはずで、変動の大きさもf倍になり、前回値を出すアルゴリズムは誤差がf倍不利なはず
- バイアスがない状態で+の領域の最大値=0.85/-の領域の最小値=-0.7という上下の非対称性があること
- +のピークが真のデータに比べて1回遅れ、-のピークが真のデータに比べて10回遅れであり、時間の非対称性があること
- 僅かだが上下に相関のないケースが残っていること
- ピークの高さは乱数が入るのでランダムだが、predictには一定の高さであること。ノイズの影響が小さい。
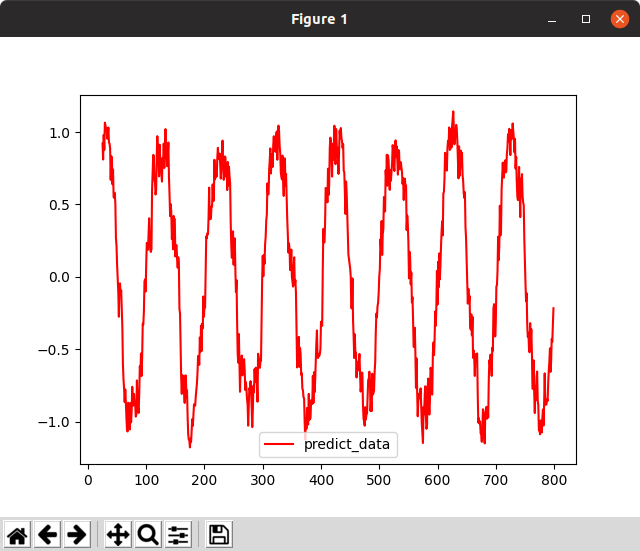
最初の仮説の極端なケースとして、周期を思いっきり下げてみよう。1/100にしてみる(振動数を早くして離散で切ると乱数になるのは複雑系界隈の常套手段)。やりすぎると収束できない。
また最後の仮説 – 8次元パラメータではピークの高さは一定になるはず – を検証するために、ノイズを増してみることを考えた。ノイズが増せば、ピークの分散が増すために、8次元パラメータ程度では学習できないに違いない。
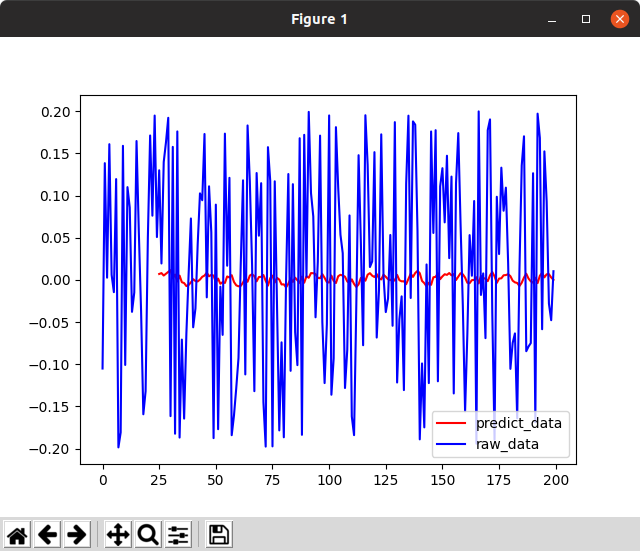
失敗(2回目・故意)
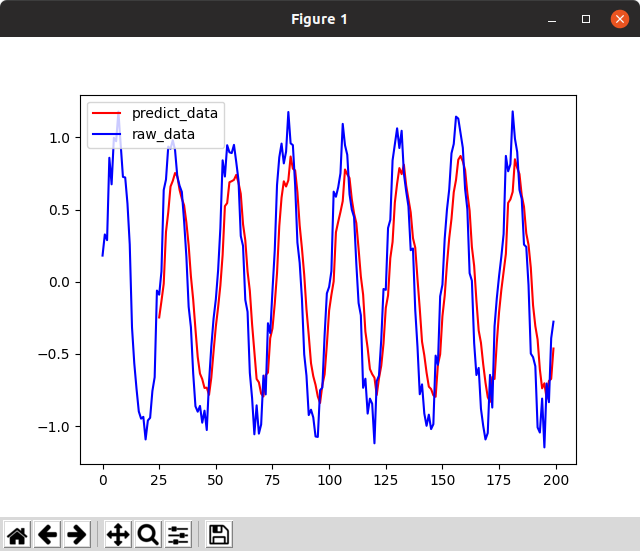
ノイズの絶対値=0.5
めちゃくちゃ怪しい。8次元パラメータで、こんなに複雑な関数が書けるだろうか。predictに使った入力データも重ね書きしてみよう。
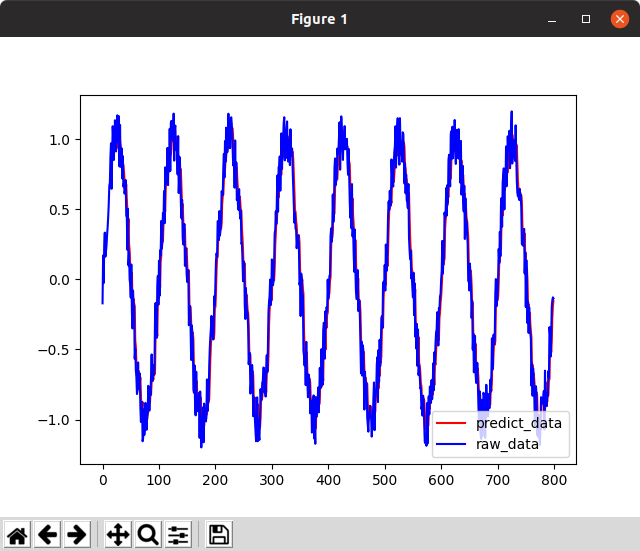
ピッタリと重なる。どう見ても前回値です。本当にありがとうございました。
ここまでで言えること
- 学習できた場合は、なめらかなカーブになる。これは、モデルが8次元パラメータしか持たず、表現力が低いためである。
- 学習できた場合は、非対称性が残る。振幅と、ピーク位置が特徴的である。
- ペナルティ項を用意していないので、epochを増やしすぎるとやはり、前回値を出力する解に陥る確率が高い。とくにノイズが大きすぎたり、サンプリングの離散度が大きくて乱数化してしまう場合。
究極のレシピ
ということは、レシピは次のようになるだろう。
- 1周期を十分な解像度で描写できるくらいの大きさの入力サイズをLSTMに持たせる。
- 周期がゆるすぎると局所解に陥るので、(ペナルティ項がない場合)、微分が十分大きくなるように周期を速くする、すなわちLSTMの解像度を落とす
- 最後に振幅及びバイアス項だけ調整する必要がある
今回、この最後の調整をdenseで行うことを考えた。やりたい「線形」変換(上下ピークのマッピング)は明確で、LSTMの中でパラメータを増やすのは非効率的だと考えたためだ。故に最終的なパラメーターは10次元となる。
成功(2回目)
こうして、再現性のある成功が得られたのだった。
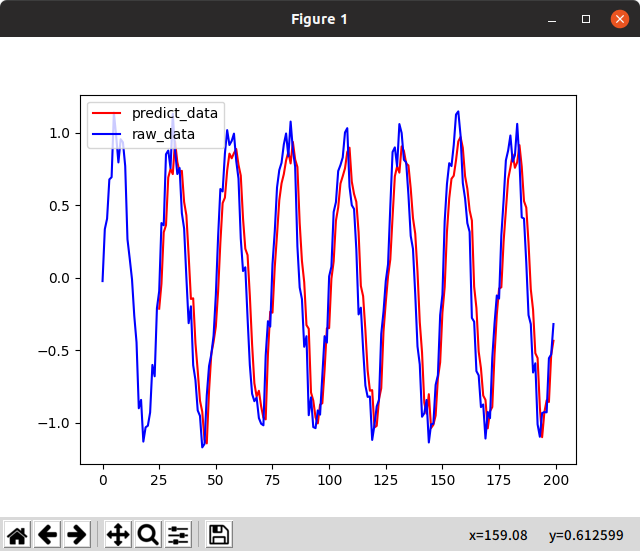
おわかりだろうか。一見前回値を出しているだけか?と思うかもしれないが、注意深く見ていただきたい。この重なりそうで重ならない感じ。上がったときに下がる、「cell値=short memory」を感じるムーブ。しかし1ユニットしかないので、2回でcell値が忘却されてしまう悲劇(Long memoryとは・・・)。これこそがLSTMである。
引き続き、LSTMに現れる宇宙の真理を追求していきたい。
参考文献
Graves最高。