レイヤー2個のLSTMは足し算を学習できるのだろうか

Table of Contents

何が問題なのか

前にMath Powerというイベントで発表させていただいたのだが、Seq2Seqというディープニューラルネットワークは四則演算を学習できる。これは、Seq2Seqが”Domain Independent”に設計されているおかげである。ただし、原論文ではSeq2Seqでは素直に学習出来ずに、reversing & short term dependencyという手法と、teacher forcingという手法と、curriculum learningという手法を組み合わせていた。つまり、かなり複雑なことをしないと学習できないという主張をしているとも捉えられる。

しかし最近理解が深まってみると、簡単な式であればそんなに大層なことをしなくても学習が可能なのではないか？という疑念が湧いたので検証を始めた。

問題設定

1hot表現という形式で数式を表現する。これは18次元のベクトルの1成分だけが1で残りがすべて0であるベクトルを数式の文字と考える表現方法だ。ただし、最後の成分”.”は文字ではなく<EOF>を表す。

list(“0123456789+-*/()=.”)

この18次元ベクトルの有限個のシーケンスを数式と考える。数式には『問題』と『答え』がある。問題は例えば

12+35=.

であり、答えとは例えば

12+35=57.

である。原論文ではnestとlengthという2つのパラメーターで問題の難易度を表すが、あえて、この形(nest=0)の足し算だけを考えてみる。すると、問題は以下のことを学習できるかと言い換えられる。

0123456789がこの順に”大きい”こと
a+b=?cの結果。例えば5+8=?3(a,b,c3個の数字の組み合わせの丸覚え)
繰り上がりを正しく行えること
<EOF>を正しい桁数で出力すること

モデル

Seq2Seqよりも大幅に単純なモデルはないだろうか？

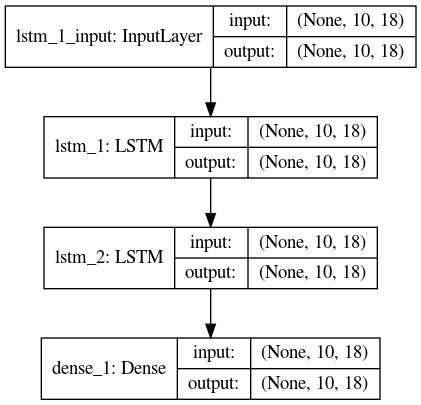
そう考えて突き詰めていった結果、最もシンプルなモデルとして、2層のLSTMで桁によらずパラメーターを共有しているものを考えた。また、1hot表現を出力しなければならないので、softmax層も必要であると考え、次の形になった。パラメーター数は5526個である。また、Noneと書いてあるのはミニバッチ入力を表している。

(8 * 2 * 18 * 18) * 2 + (18 * 19) = 5526

第一項はLSTMの項、第二項はDenseの項である。

実験結果

0.02 epoch…1問も正解しない。

0.2 epoch…ちらほら正解するようになる。

2 epoch…全問正解するようになる。

結論

つまり、問題が簡単＝nest0であれば、Seq2Seqなしに、最もシンプルなモデルとして2層LSTMを採用するだけで、足し算は学習できることがわかった。

つまり、Seq2Seqはfixed alignment以外のalignmentの学習に必要であることがわかった。

次回は、nestとネットワークの複雑性の関係を調べようと思う。

ソースコードの抜粋

可能な限り簡単にしてみた

from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import LSTM
from keras.optimizers import Adam
import numpy as np
import matplotlib.pyplot as plt
from expression import gen_expressions, decode, test_query

length_of_sequence = 10 # 12+35=. -> len=7
in_out_neurons = 18 # "0123456789+-*/()=."

model = Sequential()
model.add(LSTM(in_out_neurons, batch_input_shape=(None, length_of_sequence, in_out_neurons), return_sequences=True, activation=None, use_bias=False))
model.add(LSTM(in_out_neurons, batch_input_shape=(None, in_out_neurons, in_out_neurons), return_sequences=True, activation=None, use_bias=False))
model.add(Dense(in_out_neurons, input_shape=(in_out_neurons, ), activation='softmax'))
optimizer = Adam(lr=0.001)
model.compile(loss="categorical_crossentropy", optimizer=optimizer)

#query -> 学習データ ex) 12+35=.，answer -> 学習ラベル ex) 12+35=57.
batch_size = 100
query, answer = gen_expressions(10000 * batch_size)

model.fit(query, answer,
          batch_size=batch_size,
          epochs=1,
          validation_split=0.1,
          )

predicted = model.predict(test_query)

from keras.models import Sequential

from keras.layers.core import Dense, Activation

from keras.layers.recurrent import LSTM

from keras.optimizers import Adam

import numpy as np

import matplotlib.pyplot as plt

from expression import gen_expressions, decode, test_query

length_of_sequence = 10 # 12+35=. -> len=7

in_out_neurons = 18 # "0123456789+-*/()=."

model = Sequential()

model.add(LSTM(in_out_neurons, batch_input_shape=(None, length_of_sequence, in_out_neurons), return_sequences=True, activation=None, use_bias=False))

model.add(LSTM(in_out_neurons, batch_input_shape=(None, in_out_neurons, in_out_neurons), return_sequences=True, activation=None, use_bias=False))

model.add(Dense(in_out_neurons, input_shape=(in_out_neurons, ), activation='softmax'))

optimizer = Adam(lr=0.001)

model.compile(loss="categorical_crossentropy", optimizer=optimizer)

#query -> 学習データ ex) 12+35=.，answer -> 学習ラベル ex) 12+35=57.

batch_size = 100

query, answer = gen_expressions(10000 * batch_size)

model.fit(query, answer,

batch_size=batch_size,

epochs=1,

validation_split=0.1,

)

predicted = model.predict(test_query)