今回の目的
前回書いた、2次元データに対するHard K-means法のプログラムを拡張し、Soft K-means法(exponential decay)に変形する。
Soft K-means法は定義からはHard K-meansより性能が上昇するのかどうかわからない。実際は以下のような特徴があるので、それをこの目で確かめたい。
- Soft K-means法はHard K-means法に対して性能劣化する場合があるが、それはどの程度か?
- β→∞の極限でHard K-means法と全く同じ結果が出る
- [発展]Soft K-means法はβをパラメータとする力学系であり、混合Gaussianから生成したデータに対する固定点が、βを変化させることでピッチフォーク分岐する。この分岐図を描く。(MacKay, Information Theory, Inference, and Learning Algorithms p290 Ex 20.3)
以上を実装して確認し、Soft K-means法をより理解したい。
入力データ
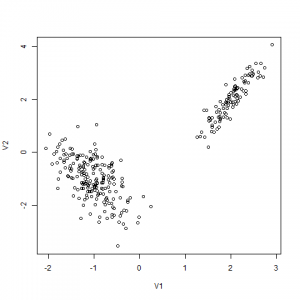
2つの2次元Gaussianの混合分布から生成します。
実際にはRで以下のように生成します。
|
1 2 3 4 5 6 7 |
> library(MASS) > x <- mvrnorm(100, mu=c(2,2), Sigma=matrix(c(0.1,0.2,0.2,0.5), 2, 2)) > y <- mvrnorm(200, mu=c(-1,-1), Sigma=matrix(c(0.2,-0.2,-0.2,0.6), 2, 2)) > write.table(x, file="hoge.csv", sep=",", col.names=FALSE, row.names=FALSE, append=FALSE) > write.table(y, file="hoge.csv", sep=",", col.names=FALSE, row.names=FALSE, append=TRUE) > z<-read.csv("hoge.csv", header=FALSE) > plot(z) |
どう見ても2つのクラスタですが、Soft K-means法はβを正しく選ばないと、このクラスタリングに失敗します。拡張したのに失敗するのは、驚くべきことだと思います。モデルを複雑にすると、抽出できる特徴は増えるが、安定性が犠牲になるというトレードオフがあるのです。この現象を過学習といい、複雑なモデルを可能な限り避けるという原理をオッカムの剃刀といいます。
(MacKay §28 ”Occum Factor”も参照)
何をするか
Hard K-means法では、各点は1つのクラスタにだけ属します。
Soft K-means法ではこれを拡張し、各点が次の重み(正規化済み)で全クラスタに属すると考えます。
プログラムの変更ですが、Pointクラスごとに各クラスタへの帰属度というベクトルを持たせます。
従来の単一帰属度(belong_to)に関するコードを全部消し、ストリーム演算に置き換えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 |
diff --git a/src/dnd/model/Point.java b/src/dnd/model/Point.java index 8800e26..5456c12 100644 --- a/src/dnd/model/Point.java +++ b/src/dnd/model/Point.java @@ -1,10 +1,16 @@ package dnd.model; import java.util.ArrayList; +import java.util.Arrays; +import java.util.Collections; import java.util.List; +import java.util.stream.Collectors; public class Point { + private static final double BETA = 100; private List<Double> coord = new ArrayList<Double>(); + private Double[] resp = new Double[0]; // Responsibility = クラスタへの帰属度 + private List<Point> clusters; // 外から渡す public int append(double newCoord) { coord.add(newCoord); @@ -15,13 +21,14 @@ public class Point { return coord.size(); } - public void add(Point point) { + public Point add(Point point) { if (size() < point.size()) { fillZero(point.size()); } for (int i=0, l=coord.size(); i<l; i++) { coord.set(i, coord.get(i) + point.get(i)); } + return this; } private void fillZero(int size) { @@ -65,4 +72,42 @@ public class Point { b.append("]"); return b.toString(); } + + public void updateResponsibilities() { + // 各クラスタとの距離を計算し、responsibilitiesに変換する + resp = clusters.stream().map(p -> Double.valueOf(exponential(this.distance(p)))).collect(Collectors.toList()).toArray(new Double[0]); + double sum = Arrays.asList(resp).stream().reduce(0.0, Double::sum); + resp = Arrays.asList(resp).stream().map(r -> Double.valueOf(r/sum)).collect(Collectors.toList()).toArray(new Double[0]); + } + + public Double[] getResp() { + return resp; + } + + public double exponential(double x) { + return Math.exp((-1.0) * BETA * x); + } + + /** + * 各クラスタに貢献ベクトルを返す。 + * @return size=clusters.size() + */ + public List<Point> getContribution() { + double sum = Arrays.asList(resp).stream().reduce(0.0, Double::sum); + return Arrays.asList(resp).stream().map(r -> this.multiply(r/sum)).collect(Collectors.toList()); + } + + private Point multiply(double d) { + Point p = emptyPoint(); + coord.stream().forEach(x -> p.append(x*d)); + return p; + } + + public static Point emptyPoint() { + return new Point(); + } + + public void setCluster(List<Point> clusters) { + this.clusters = clusters; + } } diff --git a/src/dnd/model/Processor.java b/src/dnd/model/Processor.java index 5fcbc53..0ffff8d 100644 --- a/src/dnd/model/Processor.java +++ b/src/dnd/model/Processor.java @@ -8,7 +8,7 @@ public class Processor { private final List<Point> pts; // 各点 private final List<Integer> belong_to; // 各点がどのクラスタに属するか - private final List<Point> clusters; // 平均が入る + private List<Point> clusters; // 平均が入る private final Random rand = new Random(System.currentTimeMillis()); @@ -31,6 +31,7 @@ public class Processor { } clusters.add(p); } + pts.stream().forEach(p->p.setCluster(clusters)); } public void iterate(boolean verbose) { @@ -42,36 +43,38 @@ public class Processor { private void update() { // 各点がどのクラスタに属するかを計算しなおす。 - // belong_toをアップデートする - for (int i=0; i<pts.size(); i++) { - double[] distances = distances(i); - double max = 0; - int max_idx = 0; - for (int j=0; j<clusters.size(); j++) { - if (distances[j] > max) { - max = distances[j]; - max_idx = j; - } - } - belong_to.set(i, max_idx); - } - + pts.forEach(p -> p.updateResponsibilities()); + // クラスタの平均位置を計算しなおす。 - // clustersをアップデートする - for (int i=0; i<clusters.size(); i++) { - // pts.stream().filter(p -> p > ) - Point sum = new Point(); - double num = 0; - for (int j=0; j<pts.size(); j++) { - // このクラスタに属するなら平均に加算 - if (belong_to.get(j) == i) { - sum.add(pts.get(j)); - num++; - } - } - if (num==0) continue; // 0このときはアップデートしない - clusters.set(i, sum.divideBy(num)); + Double[] total_resp = pts.stream().map(p -> p.getResp()).reduce(new Double[pts.get(0).getResp().length], (arr1, arr2) -> addArray(arr1, arr2)); + clusters = pts.stream().map(p -> p.getContribution()).reduce(getEmptyPoints(clusters.size()), (p1,p2) -> addPoints(p1,p2)); + for (int i=0,l=clusters.size(); i<l; i++) { + clusters.get(i).divideBy(total_resp[i]); + } + } + + private Double[] addArray(Double[] arr1, Double[] arr2) { + Double[] arr = new Double[arr1.length]; + for (int i=0,l=arr1.length; i<l; i++) { + arr[i] = ((arr1[i]==null)? 0: arr1[i]) + ((arr2[i]==null)? 0: arr2[i]); + } + return arr; + } + + private List<Point> addPoints(List<Point> p1, List<Point> p2) { + List<Point> arr = new ArrayList<Point>(); + for (int i=0,l=p1.size(); i<l; i++) { + arr.add(Point.emptyPoint().add(p1.get(i)).add(p2.get(i))); + } + return arr; + } + + private List<Point> getEmptyPoints(int size) { + List<Point> arr = new ArrayList<Point>(); + for (int i=0; i<size; i++) { + arr.add(Point.emptyPoint()); } + return arr; } private double[] distances(int i) { |
実行
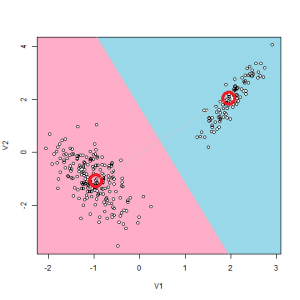
β=100で実行すると、βが大きいのでHard K-means法と同じ結果が出るはずです。しかしなんと、毎回結果が違います。絵を見ると分かるとおり、Hard K-meansの結論は、各クラス他の中心が[-1,-1], [2,2]にあるということです。
Soft K-means法を実行すると、毎回異なる結果が出ました。
正しく出るとき:
|
1 2 3 |
clusters state (time=1): [2.0120551820060375,2.0053648101847052] [-1.031528921301303,-1.0209714330131343] |
正しく出ないとき(3回の別々の実験結果):
|
1 2 3 4 5 6 7 8 9 10 11 |
clusters state (time=9): [0.03121137741693902,0.8469035051728904] [-0.05075569128262406,-0.6140780388442211] clusters state (time=9): [-1.0452866074970464,-0.9762034148700924] [1.9217817400576322,1.805404911625816] clusters state (time=9): [0.19041439198417498,-0.3389117609725727] [-0.3614591260972346,0.5304927926644216] |
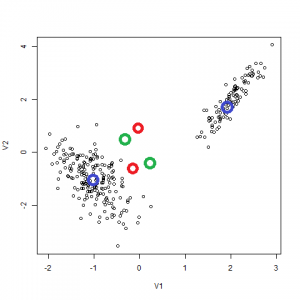
そう、これは実は正しく出てないんじゃないんです。Soft K-meansはマルチアトラクタの力学系なんです(マルチアトラクタ=安定固定点が複数あること)。
上の3つのペアを3色に色分けしたものです。この結果を見ると、必ずしも右と左でクラスタリングされているわけではなく、緑の点のように、各クラスタを半分にわけて別々のペアとくっつけたものをクラスタと機械が解釈したことが分かります。
このように、Soft K-meansを使うことでHard K-meansでは得られない特徴の抽出が出来ますが、解が複数かつ不安定になるという特徴があります。
発展
- 帰属度で各点を2色に色分けし、散布図に描けるようにする
- βに対する分岐図を描き、ピッチフォーク分岐を確かめる
あたりが次の目標です。
ピンバック: 実践:Hard K-means法2(2次元版) | The Big Computing
ピンバック: データサイエンス人気記事 - The Big Computing