エントロピーのすべて

「マクスウェルの悪魔」「熱力学第二法則」という言葉を聞いたことはないだろうか。

「部屋に閉じこもっていても酸素がゼロにならない」ことや「磁石にN極とS極があって、磁石を2つに割ってもまた磁石になる」ことを不思議に感じたことはないだろうか。

宇宙を支配する法則には「最小作用の原理」と「エントロピー最大化の原理」があり、そのうちの後者がはたらいているのがその理由である。意外なことに「エントロピー最大化の原理」は、AIの世界も支配している。

※画像はいらすとやの「ぬりかべ」で、勉強しようという純粋な気持ちをあらわしています。

Table of Contents

世界初のエントロピー

子供の頃、「いつか空気は全部和室に行ってしまって、自分は窒息死してしまうかもしれない」ということが怖かった。

大雑把に、私の家は洋室と和室が繋がっていた。空気は分子で、ふたつの部屋を行ったり来たりしている。ビリヤードのようなものだ。ではたまたま、すべての分子が和室に集まってしまった瞬間、洋室にいる自分はどうなってしまうのか？その時洋室は真空であり、宇宙と同じ状態である。ころりと死んでしまうのではないか？

人はそう簡単には死なない。エントロピーの原理に守られている。

世界最初のエントロピーはルートヴィッヒ・エードゥアルト・ボルツマン（Ludwig Eduard Boltzmann, 1844年2月20日 – 1906年9月5日)が発明した。

ボルツマンの墓には”logW”という式が刻まれている。これがエントロピーであり、ミクロカノニカルという考え方である。

どういうことかというと、空気分子が和室にあるか洋室にあるかを「コイン投げ」と考える。すると、空気分子が和室にあるという事象は確率1/2で起こる。同様に、全N個の空気分子が和室にあるという事象は確率(1/2)^Nで起こる。

Wとはこの分母のことで”状態数”と呼ばれる。よってlogW=Nlog2である。ボルツマンの理論では、この場合log(N_C_(N/2))=Nlog2(スターリングの公式で近似するとこうなる)から、ちょうど半々の分子が和室と洋室に別れるという事象しか起こりえないので人は窒息しない。

エントロピーとAI

エントロピーの考え方はなんの役に立つのか。無数の使い道があるが、まずAIに絞ろうと思う。

冒頭の例ではどんなに適当に分子運動を考えても「ちょうど半々の分子が和室と洋室に別れる」というパターンに落ち着いてしまう。よって、エントロピーはまずパターン記憶に応用された。

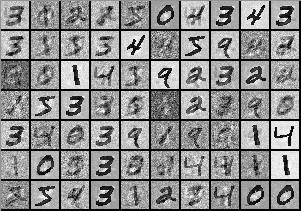
これはボルツマンマシンで数字パターンを記憶したものである。多少のノイズはあるが、数字を記憶できている。本質的には、「空気分子が2つの部屋に半々ずつ存在する状態」と、「黒い点が3の形をなしている状態」というのは同じである。ただ、ボルツマンマシンの中のパラメーター(W_ij)をいじったからエントロピー最大状態がこのような特殊な形になっているというわけだ。

ミクロカノニカル→カノニカル

これが可能な理由を補足しよう。

子供の頃、「いつか空気分子の1つがたまたまとてつもないスピードになって、矢のように突き刺さって、自分の頭が撃ち抜かれて死んでしまうのではないか」ということが怖かった。

この考えでは、冒頭では空気の位置xだけを考えたが、速度vも合わせて考えることになる。ボルツマンが考えたのは、このような様々な変数からエネルギーEを計算して、まとめてしまおうということである。この考え方をカノニカルという。

ボルツマンマシンは、各パターンの再現確率が、各パターンのエネルギーの関数exp(-E)に比例する機械学習アルゴリズムのことである。数字を記憶する例でも、各数字画像にエネルギー値が割り当てられている。数式だけ書いておこう。

$E_i = \displaystyle\sum_{j=1}^{N^2}W_{ij}x_j + b_i$

空気分子の1つがとてつもないエネルギーを持つ確率は指数関数的に減少するので、人は死なないということになり、ここでも人間はエントロピーの原理に守られている。(ちなみに、最も確率の高くなる分子速度vを計算する方法がある。マクスウェル分布をみてほしい。)

エントロピー思考

いろいろなAIにエントロピーが(無意識的に)応用されているが、AIモデルを選ぶ前に我々は解こうとしている問題についていろいろな仮説を立てて考える。このような数理的思考も、紐解いてみるとエントロピックである。

例えば人がものを買おうとしている。並べられたある商品を手に取るだろうか、取らないだろうか。これは確率的事象である。例えば、「その商品のCMへの投下予算」という変数をx、「その商品を手に取る」という変数をyとおこう。

実務ではCMに予算を投下する前に、「もしy=0が連続で1億回起きたらどうしよう？」などということは考えない。なぜなら、そのような不安は「空気が全部和室に集まって窒息したらどうしよう？」という不安と同様に、起こりえないからである。

なぜCMを行うと物が売れるのか？それは、エントロピーの原理により「典型領域」と呼ばれる事象のみが起こることが保証されているからである。(だが、大半の人間はこれを意識せずに、経験に基づいて不安を解消している)

このエントロピーを数式で明示的に計算できるデータサイエンティストは、そうでないものよりも具体的で精緻な結果を導くことができるわけである。

現存するエントロピー

単純な順から段階的に複雑なものを挙げていく。

ボルツマンのエントロピー(ミクロカノニカル)

これは、次の情報量的エントロピーの特殊な場合である。ひとつのp_i=1で、残りが0である場合に相当する。

$k \log W$

情報理論のエントロピー(ビット)

これは、コンピューターで使われるビットと同じ概念である。

$-\displaystyle\sum_{i=0}^{n} p_i \log p_i$

測度論的エントロピー(確率分布)

これは、ビットを連続空間や無限回試行に拡張したものだ。

$-\displaystyle\sum_{A_i \in \mathcal{F}} \mu(A_i) \log \mu(A_i)$

独立試行のエントロピー(マクミラン)

これは、無限回施行への極限を考える時、途中に出てくる”現実的な場合”だ。
※pは”典型的確率”と呼ばれ、典型領域の局在化によって、1/nよりはるかに大きい(→導出)

$-\displaystyle\frac{1}{n} \log p$

マルコフ過程のエントロピー(定常状態)

これは定常状態で計算したマクミランエントロピーだが、遷移行列成分が入る。なぜならば、マルコフ過程では頂点だけではなくエッジの上にも定常確率分布を考えるからだ。(→導出)

$- \displaystyle\sum_{i \ne j} \pi_i p_{ij} \ln p_{ij}$

ルールに従う時系列=力学系のエントロピー(コルモゴロフ・シナイ)

力学系ではマルコフ過程のように定常分布があるとは限らない。例えばカントール集合が定常分布になる場合があるが、測度0なので、その上での確率分布の定義は難しい。

エントロピーを計算するには空間分割が必要だが、それが時間発展する場合は逆像を計算し、逆像測度に基づくエントロピーを計算し、平均化することで求められる。

sup of

$h_{\mu }(T,{\mathcal {Q}})=\lim _{N\rightarrow \infty }{\frac {1}{N}}H\left(\bigvee _{n=0}^{N}T^{-n}{\mathcal {Q}}\right).$

力学系ルールによる逆像の測度

特に力学系がストレンジアトラクターに収束しそれが小数次元を持つときハウスドルフ次元と一致(フラクタル図形を可算個の球で被覆した時のdの下限(正の小数)。例えばカントール集合の次元は約0.63)

$arg\inf_d{\inf{\displaystyle\sum r_i^d}=0}$

ツァリスエントロピー

q!q!q!q!q!

エントロピーの本

コルモゴロフ・シナイ確率論

測度論を使った確率論の教科書。薄く、切り口が一流である。

この本はエントロピーの側面から確率的事象を理解したい人におすすめしたい。例えば、独立試行列におけるマクミランの定理は簡単で美しく、実務上も便利なのに、この本以外にはあまり載っていない。

個人的にこれを読むタイミングは3回あった。

大学4年生で物理を勉強していた時。
社会人4年目にビッグデータ分析を始めた時。
社会人10年目に人生の節目で暇ができた時、たのしみとして。

コルモゴロフとシナイの関係

コルモゴロフ(1903年4月25日 – 1987年10月20日)は測度論的確率論を作った学者。

シナイ(1935年9月21日 – )はコルモゴロフ研究室出身で、理論物理学の賞を総舐め(ボルツマン賞・ウルフ賞・アーベル賞・・・)にした学者。

2人の業績として、「コルモゴロフ・シナイエントロピー」がある。

https://en.wikipedia.org/wiki/Measure-preserving_dynamical_system#Measure-theoretic_entropy

複雑な状況でもエントロピーを計算できるようにしたという功績である。

本の概要

1~12までがモスクワ大学2年生の2学期の講義前半。13~が同じ講義の後半である。なので12が一番難しく、13でガラッと簡単になる。しかし、14から地獄の苦しみが始まる。15年読んでいるがいまいちわからないところもある。モスクワ大学にいたら2年生で落第していただろう。

p1~6
　完全加法族
p7~17
　確率変数・確率測度・チェビシェフの不等式・相関係数
p18~28
　独立試行列・シリンダー・大数の法則
p29~36
　ワイエルシュトラスの定理・典型性・エントロピー・モンテカルロ法
p37~52
　ドモアブルラプラスの定理・推定・高次元ランダムウォーク・熱力学的極限・少数の法則
p53~72
　条件付き確率・確率変数の独立性・ギャンブラー破産問題
p73~82
　マルコフ連鎖・エルゴード定理・エントロピー・正行列の無限積
p83~90
　グラフ上のランダムウォーク・高次元ランダムウォークのポーヤの定理
p91~96
　分枝過程
p97~102
　ルベーグ積分・非可測集合・ラドンニコディムの定理
p103~109
　特性関数・条件付き確率・エルミート多項式
p110~p118
　パーコレーション・臨界確率
p119~p129
　完備可分距離空間の確率論・カラテオドリの定理・特異分布関数・単関数単調極限・確率変数の非負線形汎関数・L^p空間
p130~p140
　独立同分布確率変数列・確率収束(大数の法則)・概収束(大数の強法則)・ヒンチンの定理・第1第2ボレルカンテリの定理・コルモゴロフの不等式・第1第2コルモゴロフの定理
p141~p149
　確率測度の弱収束・ヘリーの定理・プロホロフの定理
p150~p159
　確率密度関数が発散する場合の特性関数・フビニの定理・特性関数の一意性定理・特性関数の収束と確率測度の弱収束の同値性
p160~p167
　分布関数の畳み込み・畳み込みの特性関数・確率測度の弱収束としての中心極限定理・独立異分布確率変数列・リャプノフの中心極限定理・リンドバーグの中心極限定理・ガウス作用素の摂動論としての中心極限定理・ガウス分布にならない中心極限定理
p168~p174
　本質的上限下限・大偏差・大偏差の上限下限
p175~p181
　経験分布の弱収束・グリベンコの定理・コルモゴロフの極限定理
p182~p191
　ピアソンのカイ二乗検定・ピアソンの極限定理
p192~p200
　ネイマンピアソンの判定法
p201~p208
　スチューデントのt
p209~p220
　クラメールラオの限界

ツァリスエントロピーの本

q!q!q!q!q!q!q!

コルモゴロフ・シナイエントロピーとディープラーニング、あと科学とか

オタク向け情報だが、

1.DeepLearningの理解に役立つ

Adaptive Approximation and Generalization of Deep Neural Network with Intrinsic Dimensionality

まず予備知識としてここで言っている情報次元とかコルモゴロフ・シナイエントロピーとかはだいたい一致するものである。それをdとするとディープラーニングのエラーレートがdで押さえられるという・・・

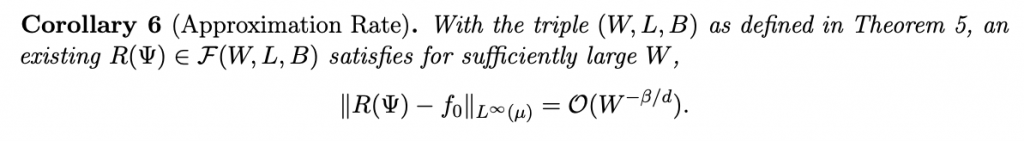
証明は理解してないのでオタク各位は頑張って欲しい。

DeepLearningがコルモゴロフ・シナイエントロピーが低い関数に向いているという研究もある。これはカウフマンのようにバイナリのネットワークを総当たりで調べる方法をとっている。

Deep learning generalizes because the parameter-function map is biased towards simple functions

2. 情報次元とコルモゴロフ・シナイエントロピー

以下の書籍に一致性が書いてある。p135あたりである。

3. チャイティン

チューリング停止問題とコルモゴロフ・シナイエントロピーが関係あるんだった気がする。

この本は「そんなの読んでたら研究者になれないゾ。めっ🌟」と佐々教授に怒られた本。実際研究者にはなれなかった(読んでなくてもなれなかったと思うが・・・)