【因果推論】”Statistical Rethinking” (R/Stan)

1件のコメント / データサイエンス、数学 / By

Statistical Rethinkingの日本語版が無いので日本語情報を書いてみました。Statistical Rethinkingは「統計を考え直そう」という意味です。Rとstan(rstan)で実用的なベイズ推定手法だけではなく、統計学に対する深い洞察が語られているのが特徴です。

※画像はいらすとや様の「ぬりかべ」で純粋な向上心をあらわしています。

どんな本？

かなりの高評価

それでは統計学の何を考え直すのでしょうか。

1.「帰無仮説を棄却することはポパーの言う『反証可能性』を満たさないがそれはなぜか？」

2.「2つの正反対の仮説が同一の統計モデルに帰着してしまうことがあるがそれはなぜか？」

3.「全てのモデルは厳密にはFalseだが、モデルを反証する(Falsify)という行為は何を意味しているのか。最初からFalseであるとわかっているのに。」

4.「なんと単回帰でさえ失敗する場合が応用上よくある。どんな場合か。」

5.「新しい科学を作る場合に統計学が使いにくいのはなぜか？とくに測定誤差が分野により異なるがそれはなぜか。」

etc…きかれたら固まってしまいそうです(続きはページ下部)。2020年の最新版が良いです。2016年の初版からは大きく内容が増補されました。

レベル感

回帰はできるが仕組みには納得していない、文系の博士課程の学生を想定しています。と著者は書いていますが、WAICが記載されていたり、Hamiltonian Monte Carloの原理が省略なく解説されていたり、かなり本格的で理系の研究者向きでも通りそうです。

とはいえ文系研究者向けなので、∫を使わないということが繰り返し語られます。しかしHMCが解説されていることからも分かる通り、著者は数式を避けているのではありません。posteriorから直接サンプリングすることで、直感的になるからです。数学的にはサンプリング理論の中にたくさん∫が入っているので、サンプリングアプローチで理解した後に、数学を学べばいいと思います。

著者はどんな人？

Richard McElreathは人類学の研究者です。若干41歳で教授、若干42歳でマックスプランク進化人類学研究所のマネージングディレクターに就いているという相当な実力者です。近年「再現性の危機」について研究しています(再現性といえば機械学習の論文の再現性)。博士課程における研究テーマは限定合理性で、ハーバート・サイモンの流れを受けているようです。

Rやstanを最初期から使い、両方の言語でライブラリを開発しています。

著者のYouTube

この本はベストセラーになったとはいえ、とても高価です(1億円以上売れているのでは？？)。しかし、YouTubeで2019年の講義(10週間・全20回)が公開されています。素晴らしい内容です。

YouTube上での講義中の彼は・・・親父ギャクを連発しています。学生は笑う時も笑わない時もあります。数話でだんだん笑いどころがわかってきます。

Lecture1 @ week1

まずはKindleのサンプルを

2020年現在、コロナの影響でイギリスからの発送が難しい状態にあります。手元に紙のコピーがない場合は、副読本としてKindleのサンプルをダウンロードすることをお勧めします。かなり太っ腹で、59ページも無料で読むことができます。Kindle版へのリンクはこちらの画像をクリックし「無料サンプルを送信」してください。

Rethinkingコレクション

この本の魅力はここ(本質的な問い)だと思います。以下の疑問に即答できたら統計完全理解者だと思います。

0.「統計学は科学でも数学でもない」

1.「帰無仮説を棄却することはポパーの言う『反証可能性』を満たさないがそれはなぜか？」

2.「2つの正反対の仮説が同一の統計モデルに帰着してしまうことがあるがそれはなぜか？」
(具体的な例としては、仮説1=適者生存、仮説2=中立進化説のとき、同一の統計モデル=べき乗則が導かれる)

3.「全てのモデルは厳密にはFalseであるわけだが、モデルを反証する(Falsify)という行為は何を意味しているのか。最初からFalseであるとわかっているのに。」

4.「なんと単回帰でさえ失敗する場合が応用上よくある。どんな場合か。」

5.「新しい科学を作る場合に統計学が使いにくいのはなぜか？」

6.「自然に指数型分布族が多いのは、自然がエントロピーを好むからである。過程の忘却は指数型分布族を導くか？」

7.「絶滅を証明するときは常に観測値が0になるが、それが間違っている確率は0ではない。測定誤差を評価せよ」

8.「なぜよくあるベイズの定理を使った病気検査の例は、ベイズ推定の説明として好ましくないのか？(それは頻度主義的だからだが、なぜそう言えるのか)」

9.「中心極限定理は無記憶性をあらわすので、過程も忘却されてしまう。統計的な分布から因果関係が言えるはずがない。指数型分布をしていない場合にはどうか。」

10.「欠損値がある時、パラメーターを1次元増やしたマルチレベルモデルと同一視が可能であることの具体例を示せ」

11.「ベイズ流に確率を定義する場合、Coxの流儀とBruno de Finettiの流儀があるので違いを説明せよ。」

12.「ロナルド・フィッシャーは1925年の著書でベイズ統計を完全否定しているがそのロジックと根拠は？」

13.「『アフリカ人以外の方がネアンデルタール人とのDNA重複が多い』という事実から、これを説明するが正反対の仮説となる因果モデル2種を考えてみよ。」

14.「階層モデルの研究が活発化したのは、実は階層モデルを用いてJohn Tukeyが1978年の選挙戦を制してからであった。(彼はFast Fourier Transformとジャックナイフ法に貢献した人物である。)」

15.「コロンブス(本ではコロンボ)が1492年に参考した地図にはアメリカとオーストラリアが無い。このとき、コロンボがベイズ推定を行っていたとした場合、アメリカをインドと考える推定結果が妥当か議論せよ」

16.「とりあえず全変数を機械学習モデルに突っ込む方法(Causal Salad)が最も高い精度を出してしまったとする。その場合精度が最高にも関わらず、深刻な失敗をもたらしうる。どんな場合か考えよ」

17.「ベイズ推定では、実は観測できなかった場合それがデータかパラメーターかを一意に決定することはできない。priorかlikelihoodかの区別についても同じことが成り立つか考えよ。」

18.「MLE(Maximum Likelihood Estimate)を行うとき、近似解を求めるためにquadratic approximation(2次のテイラー展開)を行うと失敗するが、MCMCを行うと回避できる場合がある。」

実務に追われていると、こうした点をあやふやにしてしまっているのではないでしょうか・・・だからこそのRethinkingということに意味があるのだと思います。

ざっくりとした構成

  1. 1〜5は簡単なモデル。1・2・3章がベイズ。4・5章が線形ベイズ。
  2. 6章が因果推論。Directed Acyclic Graphなど
  3. 9・10章が基礎(Markov Chain Monte Carloとエントロピー)
  4. グラフィカルモデル。11章が離散モデル。13・14章がマルチレベルモデル。
  5. 15・16章が実務上の問題点(欠損・測定誤差)

タイトルの意味・親父ギャグの解説

  1. The Golem of Prague
    プラハのゴーレム、です。ゴーレム発祥の地はプラハで、ゴーレムは額に”emet(True)”と刻むことで命じたタスクを意味を考えずに完遂します。これは、数式を刻むことで因果関係などを考えずに完遂するプログラムのようです。
    暴走したゴーレムはプラハの街を破壊してしまいますし、何も考えずに適用された統計プログラムは科学理論を破壊してしまいます。
    The Unified Theory of Golem Engineering
    この本は「ゴレーム使いの統一理論」です。まず機械学習を科学ではなくゴーレムであると認識する。多種多様なゴーレムを生み出した背景と歴史の流れを理解する。ゴーレムの挙動を常に懐疑(skepticism)する。といった理論です。
    Innovative Study
    このような統一理論が必要なのは、「新しい科学を生み出す時」です。
    往々にして、五里霧中のプロセスにおいては統計理論は適用できなかったり、無理に適用すると壊れてしまうのです。
  2. Small Worlds and Large Worlds
    コロンブスがアメリカをインドだと勘違いした話は有名ですが、ベイズ推定はこれに似ています。当時知られていた国の知識から最も尤もらしかったのは、インドだったのです。現実の世界にはアメリカ大陸やオーストラリア大陸がありますから、その知識があれば、コロンブスの推定は違ったはずです。
    限られたデータで間違った推定を行うことをSmall World、現実の世界でその推定が問題を引き起こすことをLarge Worldに例えています。
    The Garden of forking
    「分岐の庭」はボルヘスの小説で、日本語訳はされていないようです。ボルヘスの「砂の本」には日本語訳がありますが、似たテイストの小説です。ネタバレはこちらで読めます。
    Water and Land
    Head/Tailでなく、コイン投げの代わりに地球投げが行われます。W=0.7、L=0.3の確率で起こるようです。
  3. Sampling the Imaginary
    Imaginaryとは、パラメーター空間のことです。統計モデルが現実ではない以上、統計モデルのパラメーターに対応するものは現実のどこにもありません。ベイズ回帰を行う場合は、パラメーターは確率分布からサンプリングしますが、あくまでこのサンプリング自体は現実と何の関係もないことを意識しましょう。
    Frequentist
    ところでこの”Imaginary”には、頻度主義への皮肉が込められています。
    ベイズ推定は「主観的統計学」と揶揄されることがあります。priorの選び方などに必然性が無く、Imaginaryと呼ばれるように現実に対応しないような変数がたくさんあるからです。例えば確率pは頻度主義においては多数回の観察の漸近値であり、一通りしか無いのにもかかわらず、ベイズ推定ではpは確率というにはかなり自由(確信度つき)でありあらゆる値をとって良いのです。
    しかし、頻度主義は別の意味で非現実的なのです。なぜなら、頻度主義のあらゆるパラメータ(例えば、信頼区間)は多数回観察の漸近値(Asymptotic)であり、例えば信頼区間ひとつとっても、信頼区間を1000回以上計算して漸近値を出すことを想定しているからです。これこそ”Imaginary”ではないか、と著者は批判しています。
  4. Geocentric Models
    これは地球中心説＝天動説のことです。天動説ではエピサイクル・エカントを使って、小文字のγの形のような惑星軌道を説明できます。
    仕組みとしては、エピサイクルと呼ばれる小円を追加するたびにフーリエ係数が増えていくことになるので、無限に良い近似ができます。
    著者は天動説と回帰は「ある場合には精度の高い近似が可能だが、根本的なメカニカル理解が間違っているモデリング」という意味で同じだと考えています。
    そして、新しい科学を創る立場は天動説で宇宙に挑んだプトレマイオスと同じであり、未来にわかるメカニズムとは別に、優れた近似の方法が必要だとしています。熱いですね。
    Spline
    例えばスプライン補間は、Geocentricモデルであり、科学ではなく近似だ、と語られます。
    Wiggly
    「くねくね」という意味。時系列のグラフをフィッティングする話です。１０００年以上記録が残っているという日本の桜開花日を使います。crazy…
  5. The Spurious Waffles
    ワッフル屋さんの数を使って、その州の離婚率を推定することができます。これは、偽の相関(Masked Relationship)についての話です。Spuriousはあやしいという意味です。
    Waffle House Index
    しかしながら、実は「ワッフル屋さんが営業しているかどうか」は実際に真の説明変数として利用されたことがあります。
    2011年のハリケーン災害において、災害化でもワッフル屋さんは営業をいち早く再開しており、電気水道ガスなどが破損していない目安とされたのです。なるほど、確かにレストランが復旧するためには、野菜の配達を待ったり、電気水道ガス以外のインフラが復旧することが必要ですが、ワッフルを焼くのにそれらは必要がありません。よって、ワッフル屋さんが一番営業再開しやすいのです。そのため、ワッフル屋さんが臨時閉店している地域が重要災害地区であるとして優先的に対応されたのです。
    ゆえに、ワッフルハウス指数は、同じ変数が偽の相関であったり真の相関であったりするという稀有な例なのです。
  6. DAG(Directed Acyclic Graph)
    Acyclic＝ループしないという意味です。dagittyというRのライブラリを使って描画します。そのほかにも、一貫性のある候補を提示させるなど多少の計算ができます。
    Berkson’s Paradox
    美味しくない店は場所がよくないと生き残れない、美味しい店は場所が悪くても生き残れる、淘汰の結果目につく店は全部不味くなるという法則です。
    Collider Bias
    X→Y←ZのDAGにおいて、Yによる条件付確率を計算してしまった時にBerkson’s Paradoxを起こしてしまうバイアスのことです。
    Simpson’s Paradox
    母集団で存在しない相関が、分割全てで見られる現象です。例えば、52枚のトランプのうち20枚が無作為に汚れてしまったとします。この20枚を分析したところ、赤は13枚/黒は7枚だったとします。さらに分析したところ、赤の絵札は4枚/黒の絵札は2枚だったとします。
    このとき、汚れたトランプを分析すると「赤の方が絵札率が多い(4/13>2/7)」が成り立ちます。
    また、汚れてないトランプを分析すると「赤の方が絵札率が多い(8/13>10/19)」が成り立ちます。
    よって、トランプ全体でも「赤の方が絵札が多い」と言えます。(言えません！)
    Confound
    この章の最重要単語です。偽の因果関係のことです。(偽の相関ではない)
    「因果関係がごちゃごちゃになる」という意味です。観測できないが因果関係に影響を与えてしまう変数があると、それをBackdoorにして情報が流れてしまう現象が起きるのが原因です。日本語では交絡(こうらく)ともいいます。
    Backdoor
    主にコリダーバイアスによって情報量が漏れる経路のことです。shut downすることが出来ます。
    Haunted DAGs
    この本通しても、最も実務上役立つ概念です。
    全てのDAGの全てのEdgeに対応する2点には、観測不可能な変数が同時に影響を与えることが理論上可能です。ということは、どのようなDAGも、nC2通りのConfoudを見落としているリスクに付き纏われている(Haunted)と言えます。つまり因果のDAG表現は、全てのConfoundが存在しないかの絶え間ないチェックと組みなのです。
  7. Ulysses’ Compass
    ユリシーズはオデュッセイアの現代版といった趣の、1920年代の小説です。オデュッセイアは航海と冒険の話でコンパスが出てきます。カリュブディスか、スキュラか選べて戦えるという罰ゲームのような海峡が出てきます。当然どっちもいやです。OverfittingとUnderfittingを避けよう、というのがユリシーズコンパスの意味です。
    Occum’s Lazerの原理に従うと、Underfittingになりがちです。それではダメです。なので、Occum’s LazerとUlysses’ Compassの違いを理解しましょう、ということです。
    Golem taming
    ゴーレムを飼いならす、という意味ですが、、、Overfittingをやめさせることです。ゴーレムはデータに敏感すぎるので、「鈍く」してやります。
  8. Conditional Manatees
    マナティの背中は、ボートのプロペラに巻き込まれてズタズタになります。痛ましい写真に、感情が揺り動かされます。
    では、ボートのプロペラを安全にすることで、マナティは感謝するでしょうか？
    実は、マナティのほとんどはボートの竜骨に当たって即死してしまうのです。即死したマナティは海の底にしずみ、観測されることはありません。
    そう、私たちが見ている痛ましいマナティは、全て条件付き確率分布からサンプリングされたマナティなのです。故に、これを学習データにしてしまうと過学習がおきます。
  9. Good King Markov and Good King Monty
    優しい王様であるマルコフは、各島の人口に比例して滞在しようと頑張ります。MCMCの擬人化です。
    はっちゃけた王様であるモンティは、国から国をバイクで駆けまわります。運動エネルギーを持っているので、Hamiltonian Monte Carloの擬人化です。
  10. Big Entropy and GLM
  11. God Spiked Integers
    Poisson Regression
    博士課程の応募率は熱力学極限であるという親父ギャグがあります。
  12. Monsters and Mixtures
    Monsters
    階層ベイズモデルは無根拠かつ無限に複雑に出来るので、キメラのようなモンスターに例えられています。
  13. Models with Memory
    Reed Frog
    この章のテーマは記憶のプーリングです。なぜ蛙が題材なのか。Pool(水たまり)と蛙をかけたのでは？
  14. Adventures in Covariance
    Unpopular cafe
    人気があるカフェは平均売上も、朝夕の売上差も大きい。
    人気がないカフェは平均売上も、朝夕の売上差も小さい。(一般的には朝はお客さんが多いので忙しくなるが、そもそも朝も夕方もお客さんが来ない)
    このことから、機械学習モデルのパラメーターは独立でなく、共分散が重要であることがわかる。なぜなら、切片(intercept)と傾き(slope)が連動しているからである。
  15. Missing Data and Other Oppotunities
  16. GLM(Madness)
    Geometric People
    Ordinary Differential nut cracking
    ODE(Equation)ならば微分方程式のことですが、、、
  17. Horoscopes
    黄道十二宮で有名な天体図のことです。この章は3ページしかありません。

練習問題解答

てこずったものだけ

2H(Hard)1

問題：「パンダAは10回に1回、パンダBは10回に2回双子を生む。見た目では区別がつかない。あるパンダが双子を生んだ。次も双子を生む確率は？」

答え：「16.666…%」…だと思います。10%と20%の平均の15%にはならない。

求めたいものは、P(2nd=twin | 1st=twin)。priorはP(A)=P(B)=0.5。よって

P(2nd=twin && 1st=twin)
=P(2nd=twin && 1st=twin | A)P(A) + P(2nd=twin && 1st=twin | B)P(B)
=P(twin | A)^2 * P(A) + P(twin | B)^2 * P(B)
=0.025

P(1st=twin)
=P(1st=twin | A)P(A) + P(1st=twin | B)P(B)
=0.15

の比を取れば良い。

2H2

問題：「同じ設定でパンダが双子を生んだ。パンダがAである確率は？」

答え：「33.333…%」だと思います。

P(A | 1st=twin) = P(1st = twin | A) * P(A) / P(1st=twin)

2H3

問題：「同じ設定でパンダが1回目は双子を、2回目は1頭だけ産んだ。パンダがAである確率は？」

答え：「36%」だと思います。0.5の確率で双子を産むパンダに近いのはBなので妥当です。

P(A | 2nd=singleton, 1st=twin)
=P(2nd=singleton | A) * P(1st=twin | A) * P(A) / {P(2nd=singleton | A) * P(1st=twin | A) * P(A) + P(2nd=singleton | B) * P(1st=twin | B) * P(B)}

3M(Middle)3

問題：「地球投げで15回中8回Waterが出たとする。GridApproximationでposteriorを求めよ。次にこのモデルを検証せよ。つまり異なるpを持つモデル群をposteriorで平均化し、15回投げる試行を各モデルに対し多数回行い、平均して最も『8回』の頻度が大きくなることを確かめよ。」

posteriorで積分するよりも、posteriorからpの列をサンプリングし、そのリストを生成関数に使わせるのが賢い。

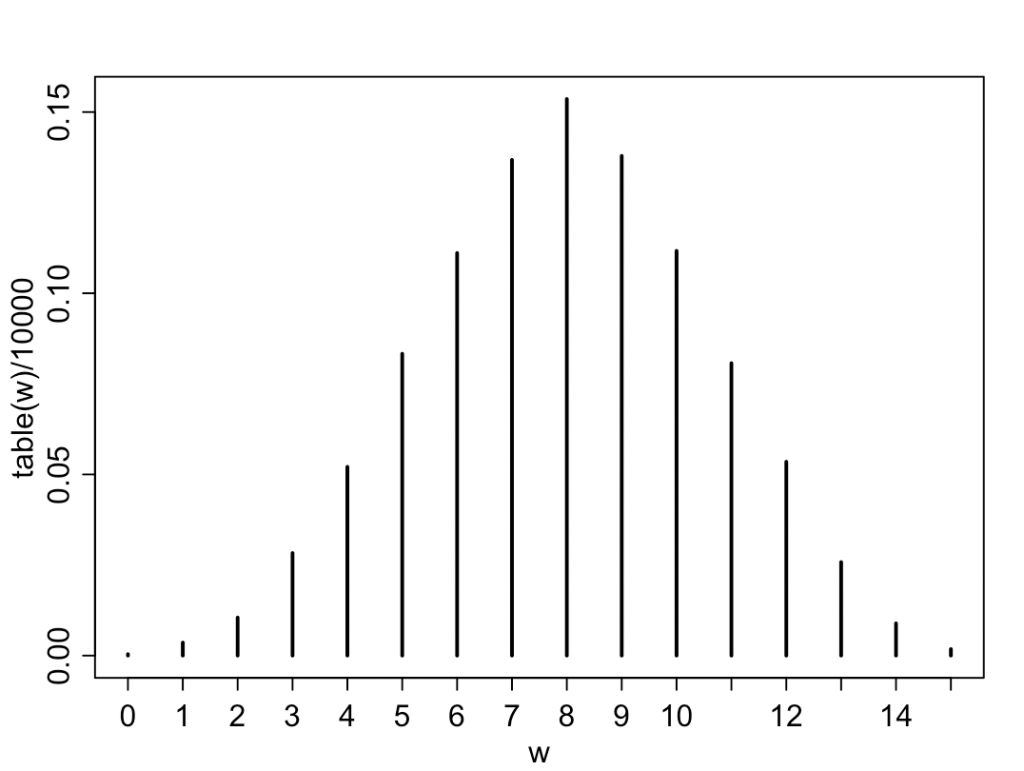
確かに、W=8回(W+L=15回中)が最も確率が大きく(15%)なり、整合性が取れている。

3M4

同じコードの引数を変えるだけで、「9回中6回がWである確率」を出せる。答えは約17.29%(シミュレーション値)。2項分布ではない点に注意。

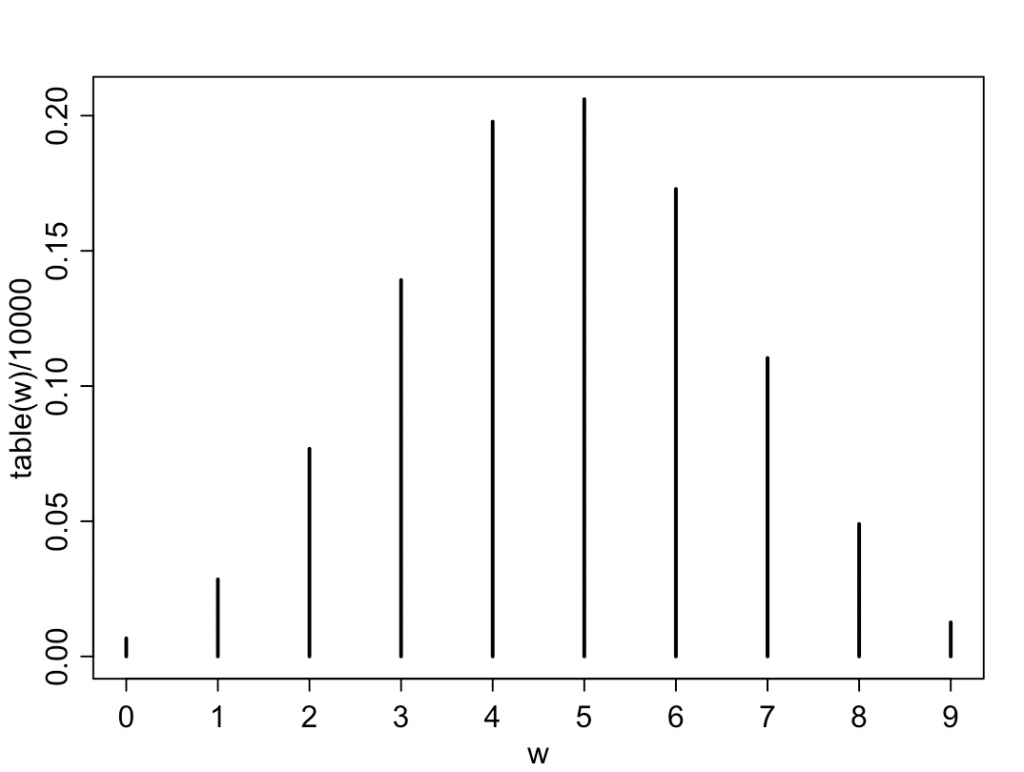
3M5

「前もって地表の50%が海だとわかっているとして、モデリングをしなおせ」

すると、今度はposteriorによる平均化後の最大確率が9回となり、8回では無く、整合性が取れていない。これは、priorとデータが整合していないからである。

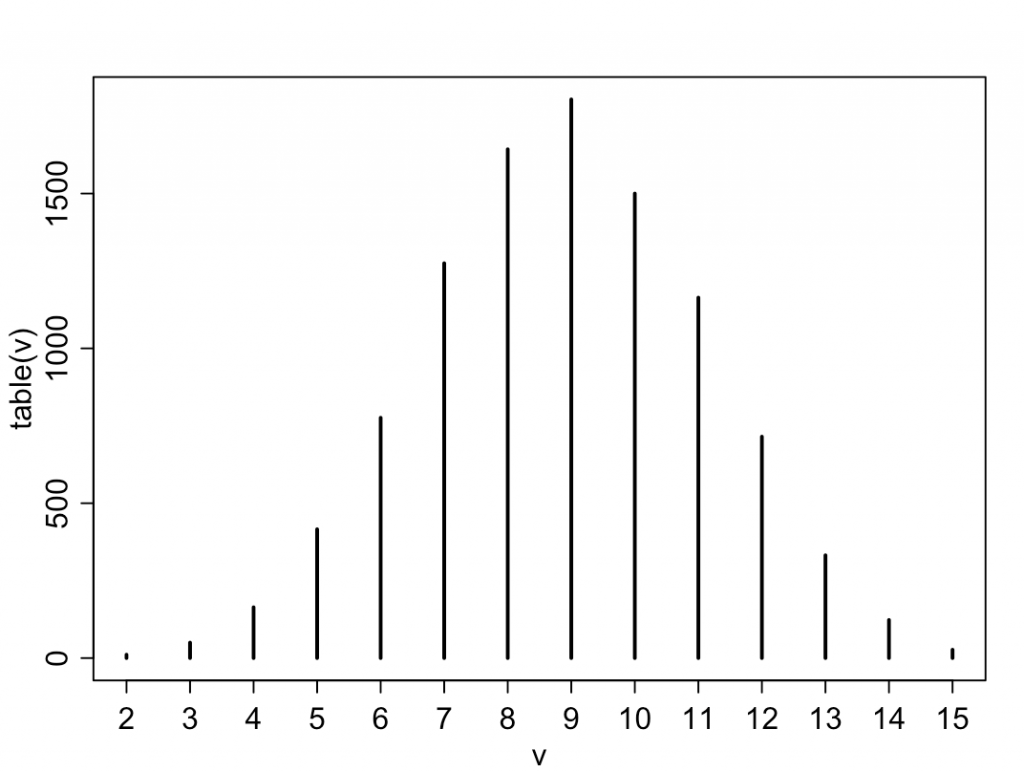
3M6

「地表のWater率を精度高く見積もる場合、何回投げれば良いか。95%のPercentile Intervalが、5%以内の幅に収まるようにしたい。」

本文には現れませんが、この幅はドモアブル・ラプラスの定理より√Nに反比例します。以下のコードで幅が小さくなっていくのを確かめられます。

3H5

結論としては、第一子が女性である場合、第一子と第二子の性別は独立ではない。（第一子が女性だと、第二子は男性である確率が高くなる。）

これを証明するコード

ここから、49人中男子が39人になる事象は、0.1%未満であり、モデルが正しくないことがわかる。

休憩に読む本

「【因果推論】”Statistical Rethinking” (R/Stan)」への1件のフィードバック

  1. ピンバック: 統計検定チートシート(1級・2級) | The Big Computing

コメントは受け付けていません。