Latent Dirichlet Allocationを提案したBleiの論文のAbstract~Section 1を和訳したものです。原論文はgoogle scholarで読めます。(リンク)
Table of Contents
原論文:Abstract
LDAは、生成モデルであり、テキストコーパスのような離散データを対象とする。
LDAは、3層の階層ベイズモデルで、各アイテムを潜在的なトピックの重ね合わせとしてモデリングする。逆に各トピックは、トピックの確率分布の重ねあわせとしてモデリングされる。
テキストモデリングの文脈で、トピックの確率はドキュメントの表現を与えると考えられる。
我々は、変分ベイズ法とEMアルゴリズムに基づいた効率的な近似的推論アルゴリズムを示す。
我々は、ドキュメントモデリングの結果と、テキスト分類、協調フィルタリングの結果を提示し、ユニグラムモデルやLSIモデルとの比較を行う。
1. Introduction
この論文ではテキストコーパスやその他の離散データの問題について触れる。
目標は、効率的な処理を可能にする一方、テキスト分類やノベルティ検出、要約、類似性や関連性判定といったことを可能にする統計的性質を壊さないような、データ表現を見出すことである。
この問題については、IRの分野でかなりの発展が見られる。
基本的な方法は、インターネット検索で実用されているもので、各ドキュメントを単語回数ベクトルに変換するというものである。
有名なTF-IDF法では、基本的な語彙がまず選ばれ、コーパス中の各ドキュメントに対して、単語の生起回数が数えられる。適当な正規化の後、この生起頻度はドキュメントの頻度の逆数をかけられる。ドキュメントの頻度は、コーパス全体にこの単語がどれだけ現れるかの尺度である(通常対数をとって正規化される)。
結果は単語-ドキュメント行列となり、各カラムが各ドキュメントに対するTF-IDF値を格納する。
よって、TF-IDF法はドキュメントを固定長のベクトルに変換できる。
TF-IDFには魅力的な性質がある。特に、ドキュメントを特徴づける単語の集合を特定できる点である。このアプローチはドキュメントをかなり小さいサイズに変換できるが、ドキュメント間の統計的関連性についてはほとんど明らかにしない。
この結果を説明するために、IRの研究者は他の次元縮約法を見出した。最も有名なのは、Latent Semantic Indexing(LSI法)である。
LSIは行列の特異値分解を使って、TF-IDF法の特徴空間の部分空間を得る。その部分空間は、最も分散の大きい部分に対応する。
このアプローチは、大きなデータをかなり圧縮する。しかも、DeerwesterらはLSIが導き出した特徴ベクトルは、TF-IDFの特徴ベクトルの線型結合だが、synonymy(同義語)やpolysemy(多義語)などの言語的特長を表現していると主張した。
このLSIの主張を実証するため、またLSIの強みと弱みを調べるためには、確率的生成モデルを使ってテキストコーパスを分析し、LSIが生成モデルの性質をデータから再現できるかを見るのが有効である。
しかしテキストの生成モデルが与えられても、なぜLSI法を採用すべきかは自明とは言いがたい。むしろ直接的に、最尤推定やベイズ推定を使ってフィッティングすることも出来る。
この方法を大きく発展させたのはHofmann(1999)で、確率的LSIモデル(別名アスペクトモデル)を提示した。pLSIについては§4.3で触れるが、ドキュメント中の各単語を多項分布の重ねあわせからランダムサンプリングする方法である。この多項分布は”トピック”であると解釈される。
だから単一トピックから各単語が生成され、ドキュメント中の異なる単語は異なるトピックから生成されているかもしれない。各ドキュメントは複数のトピックの混合されたもので、トピック集合の上の確率分布だと考えられる。この確率分布はドキュメントの”縮約表現”と呼ばれる。
Hofmannの研究がテキストの確率的モデリングに一石を投じたとはいえ、pLSIはドキュメントレベルでの確率モデルを構成できない不完全なものである。
pLSIでは各ドキュメントは数のリストで、これらの数を生成する確率モデルを持たない。
これにより以下の問題が生じる。
- モデルのパラメータの数がコーパスのサイズに線型に比例し、過学習を起こす
- ドキュメントに対してどう確率を割り当てるかが決まっていない。
pLSIの先に行くためには、次のような基礎的な確率に関する要請を行う。この要請は、LSIやpLSIなど、次元縮約を行うモデルにつきものである。
それは、ドキュメントが”bag-of-words”であるという要請である。つまり、ドキュメント中の単語の順番は無視して構わないと言う前提を置いている。
確率論の言葉では、ドキュメント中の単語の置換にたいする不偏性の要請と言える。
さらに、明示されることは少ないとはいえ、これらの方法はコーパス中のドキュメントの順番も無視して構わないと言う前提を置いている。
de Finetti(1990)にさかのぼる、古典的な表現定理では、置換可能な確率変数は、無限個の確率分布の混合分布で表現されるとしている。
だから、もしわれわれがドキュメントや単語を置換可能とするなら、混合分布モデルを考えなければならない。
この考えに従ったのが、我々の提案するLatent Dirichlet Allocation(LDA)である。
最も強調されるべきは、この置換可能性は確率変数の独立性や一様分布性を意味しないと言うことである。むしろ、置換可能性は”条件付き独立かつ一様分布”と解釈できる。それは、潜在変数(latent variable)についての条件付き確率分布である。
条件付きで、これらの確率変数の同時分布は単純かつ分解可能になる。ただし、潜在変数で周辺化した場合、複雑かつ分解不能になることに注意すべきである。
だから、テキストモデリングの分野では置換可能性は単純化を意味し、計算が効率的に可能であることを意味するが、必ずしも単純な頻度確率や線型操作を意味しない。
我々の目的は、de Finettiの定理をこれらの混合分布に真面目に適用すると、ドキュメント間の統計的関連性を捉えることが出来ることを示すことである。
また、このことにも触れておかなければいけない。置換可能性の一般化はたくさんある。その中には部分置換可能性もあり、表現定理も同様に適用できる。
だから、我々のモデルが”bag-of-words”モデルしか扱っていないとはいえ、我々の方法はもっと順序を考慮したモデル、例えばn-gramや段落モデルにも適用できるはずだと言うことである。
この論文の構成は次の通りである。§2では基本的な用語や表記法を導入する。
LDAモデルは§3で登場し、§4で関連のある潜在変数モデルと比較される。
パラメータ推定については§5で議論される。
目覚しい成果、LDAをデータにどう適合させるかについては§6で扱う。
テキストモデリング、テキスト分類、協調フィルタリングについての実験結果は§7で提示される。
最後に、§8で結論を述べる。
補足:Latentモデルとは
LatentモデルとはLatent変数を持つモデルです。Latentとは潜在的、という意味で、隠れ変数とも呼ばれます。直接は観測できないが、モデルに存在する隠れ変数のことを意味しています。
もっとも有名なLatentモデルは、Gaussian Mixture(GMM)です。これは、データ点の分布が、いくつかの正規分布から生み出されると仮定します。
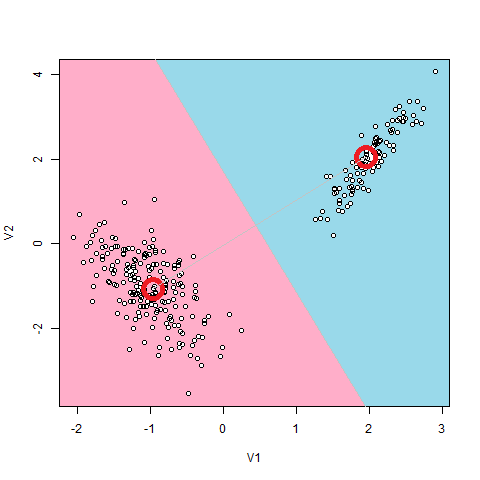
例えば上図のように、2つの塊になっている点分布の場合、2つの正規分布からデータが生成されていると仮定するのが自然でしょう。
このモデルにおけるLatent変数とは、2つの正規分布のどちらから生成されたのかという2つの値をとりうるカテゴリカル変数です。これらは、データ1個1個から直接は観測できない変数になっています。
補足:LDAにおけるLatent変数
LDAのLatent変数は、Dirichlet分布に従う「トピックID」です。
例えばLDAで文章を解析する場合、文章の主題の種類をトピックといいます。例えば、タイガーウッズが不倫をしているという文章があったとします。
タイガーウッズは〇〇大会で輝かしい実績を残した。(文章A)
そのタイガーウッズが△△と不倫をした。(文章B)
タイガーウッズは来月に□□大会を控えている。(文章C)
架空のニュース
この場合、文章AとCのトピックはゴルフ、文章Bのトピックは不倫と言えます。
このことはLDAでは、その文章が「ゴルフについてなのか」「不倫についてなのか」という2択を表す隠れ変数がDirichlet分布に従うように、モデリングしていることになります。
その意味で、正規分布の混合分布のLatent変数と同じカテゴリカル変数といえます。