統計検定2級2021年過去問の解説です。
公式リンク
解答と解説
問1（ヒストグラム ）
縦軸の数字の頻度表（ヒストグラム）を描き、左右対称性をみます。0前後の小さい値の頻度が多いので、左にピーク、右に長い裾のヒストグラムになります。
歪度は3次モーメントを含む項で、正の値が多いので、正になります。 →目次に戻る
問2（相乗平均）
年平均成長率（CAGR）とは、成長率の1年あたりの相乗平均（幾何平均）です。 →目次に戻る
問3（パーシェ指数・ラスパイレス指数）
パーシェ指数は価格は昔、量は最新。「昔は同じ量をあんなに安く買えたのにな〜」
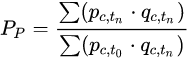
ラスパイレス指数は価格は最新、量は昔。「昔に比べて単価上がったな〜」
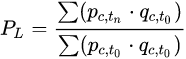
| X数量 | X価格 | Y数量 | |
| 98 | 78 | 100 | 84 |
| 80 | 80 | 70 | 90 |
| パーシェ分母 | 12120 | ラスパイレス分母 | 16044 |
| パーシェ分子 | 12700 | ラスパイレス分子 | 16840 |
| パーシェ | 1.047854785 | ラスパイレス | 1.049613563 |
問4
4の解説→東京都(1990年)は6747980部の売上なので、これを100として55まで売上が落ち込んだので45%分の3036591部減少した、となります。
5の解説→各グラフごとに特徴的な点を見つけ、それがありえないような動きであったら除外、を繰り返します。 →目次に戻る
問5（相関係数）
6の解説→1については、データの散布の幅がおよそσなので、分散σ^2の大小を判断できます。
2については、回帰可能である（つまり、データの形が直線状に近い）ほど、相関係数の絶対値は高くなります。
3については、x=0の値=切片を求めればOKです。
7の解説→飛距離点は2*飛距離xなので、共分散の定義と分散の定義に当てはめます。相関係数については、共分散と分散を使って定義した式に代入すればわかります。 →目次に戻る
問6（相関係数）
標本分散ではなく、不偏分散が与えられています。不偏分散は標本分散より少なめ、この場合だと9/10になります。 →目次に戻る
問7（抽出）
部が選ばれれば、部長は必ず選ばれる点がポイントです。 →目次に戻る
問8（確率変数）
問題文では同時確率P(X, Y)が与えられていますが、これを同時確率P(X^2, Y^2)にします。
| X\Y | -1 | 0 | 1 |
| -1 | 0 | 1/4 | 0 |
| 0 | 1/4 | 0 | 1/4 |
| 1 | 0 | 1/4 | 0 |
| X^2\Y^2 | 0 | 1 |
| 0 | 0 | 1/2 |
| 1 | 1/2 | 0 |
次に、分散・共分散を計算し、相関係数を算出します。
| X^2 | Y^2 | P | Covへの寄与=P(X^2,Y^2)(X^2-μX^2)(Y^2-μY^2) | V(X^2)への寄与=P(X^2,Y^2)(X^2-μX^2)(X^2-μX^2) | V(Y^2)への寄与=P(XX,Y^2)(Y^2-μY^2)(Y^2-μY^2) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0.5 | -0.125 | 0.125 | 0.125 |
| 0 | 1 | 0.5 | -0.125 | 0.125 | 0.125 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| Cov | V(X^2) | V(Y^2) | |
| 寄与分の合計 | -0.25 | 0.25 | 0.25 |
問9（補集合の確率）
「1-(全員の誕生日が違う確率)」です。 →目次に戻る
問10（正規分布・白色化）
正規分布の下側確率表が無いと解けないのか？と質問を受けましたが、はい、解けません。ですから、必ず問題冊子の末尾に表がついています。 →目次に戻る
問11（累積分布関数）
累積分布関数を微分すると確率分布になります。xを微分すると1なので、今回は一様分布です。
期待値は積分で計算します。
問12（チェビシェフの不等式）
問題文の式と、チェビシェフの不等式をよく比較すると、
問13（一致推定量・不偏推定量）
- 推定量は、確率変数を使った数式なので、それもまた確率変数です。
- 統計検定2級はなぜか確率収束の概念について正しく教えてくれないので、一致推定量は確率収束とまる覚えする必要があります。
- 一致推定量は確率収束で、不偏推定量は期待値の等式なので、似てすらいない全く別のものです。 →目次に戻る
問14（不偏推定量）
18の解説
μ_1~4全ての期待値を計算するしかないです。
μ_4については、
問15（信頼区間）
公式
統計検定2級では、信頼区間を逆関数やt分布から計算する方法は教えてくれないので、公式をまる覚えする必要があります。習うより慣れろと言うことだと思います。 →目次に戻る
問16（回帰）
回帰は通常y=bx + a + εですが、この問題ではa=0という制約のもとでy=bx + εという回帰を行うので、回帰の公式は使えません。
二乗誤差の関数をbで偏微分し、極小値を求めます。
状況としては、「原点を通る直線のうちどれが二乗誤差を最小にするのか」という問題を解いているので、二乗誤差は最小化されません。
これはバイアスバリアンストレードオフの状況で、バイアス(a)を小さくしたことで、バリアンス(二乗誤差)が大きくなってしまっています。 →目次に戻る
問17（信頼区間・仮説検定）
[1]は公式に代入するだけです。
[2]のアは1から残りの確率を全部引くだけです。
イはX=7と8の確率を足せば良いです。
ウはX=0,1,7,8の確率を足せば良いです。
IIが難しいかも知れません。
二級では確率収束(弱収束)の解説がされないにも関わらず、これは正しいです。
一致性とは、サンプル数が大きいときに100%正しい推定が出ることです。
ただし、期待値が真の値に一致するわけではありません。
詳しくはこちらの記事もどうぞ。
問18（t検定）
アは分母が不偏分散ではなくただの分散なので、正規分布に従います。
正規分布の線形和なので、再生性より正規分布になると考えると分かりやすいかも知れません。
イはXの2乗の和なのでカイ二乗統計量ですね。
アとイの比をとるときには当然分散であるカイ二乗統計量のルートをとって、偏差に直す必要があるので答えは②です。
問19（カイ二乗検定）
これはカイ二乗統計量の公式に代入するだけですね。実験は一回なので自由度1。
ウは自由度1のカイ二乗分布表から出せます。
問20（第1種過誤・第2種過誤）
第1種過誤は、「帰無仮説が実際には真であるのに棄却してしまう確率」です。
今回は、X1とX2がたまたま大きく離れてしまう確率です。
まず公式よりV(aX+bY)=a^2V(X)+b^2V(Y)=2です。
なので、σ=√2ですから、2.5%点を求めていることになります。
5/3%点は、正規分布表から求めます。
問21（分散分析）
ランダム化実験はとにかく可能な限り全部ランダムにすれば良いです。
分散分析の自由度は各データの数から1を引いたものになりますが、不偏分散と同じ理屈で、残差εの期待値が0になるように拘束条件があることで1減ってます。
信頼区間は公式を使えば出ます。
問22（有意検定）
重力モデルと言われる積を使ったモデルです。両辺対数をとると回帰になります。
定数項については、p=0.01に対応するtを選びます。
変数の意味があるかどうかは、基本的にstd errorが多ければ信用に値しないと考えればOK。p値はそれを定量化しただけです。
最後の問題はIのみ難しいですが、よく見るとlog(1人あたりの所得)についてはp=0.08で、5%有意でないにも関わらず採用されています。
ピンバック: 統計検定チートシート(1級・2級) - The Big Computing