弦理論の世界へようこそ！

学生さん、数式、数式をひとつずつ解きなよ。

それが、簡単すぎも、難しすぎもしない、ちょうどいいってことなんだ。

Table of Contents

弦理論の数式1（計量）

$ds^2=dx^2+dy^2+dz^2$

この式は、「計量」と呼ばれる式で、空間の2点間の長さ(ds)の2乗を表す式です。

自明な例

(1,2,3)と(2,3,4)の間には、次の関係式が成り立ちます。

$ds^2=dx^2+dy^2+dz^2=1^2+1^2+1^2=3 \therefore ds = \sqrt{3}$

追加で書くこと

極座標の例
SO(3)の作用
直交行列の作用

弦理論の数式2（ミンコフスキー計量）

$ds^2=-c^2dt^2+dx^2+dy^2+dz^2$

この式も、「計量」の一種ですが、マイナスの項を含み、時空の2点間の長さ(ds)の2乗を表す式です。

自明な例

(1,2,3,4)と(2,3,4,5)の間には、次の関係式が成り立ちます。

$ds^2=-c^2dt^2+dx^2+dy^2+dz^2$

この式も、「計量」の一種ですが、マイナスの項を含み、時空の2点間の長さ(ds)の2乗を表す式です。

弦理論の数式3（曲がった時空の計量）

$ds^2=g_{00}dt^2+g_{01}dt dx+g_{02}dt dy+g_{03}dt dz+g_{11} dx^2+g_{12}dx dy + g_{13}dx dz + g_{22} dy^2+g_{23}dy dz+g_{33} dz^2$

この式は、ミンコフスキー計量を一般化したものです。

gに(0,1,1,1)を代入すればユークリッド空間の計量になります。
gに(-c,1,1,1)を代入すればミンコフスキー時空の計量になります。

この式は、次のような対称行列を使うと、より簡潔に表すことができます。

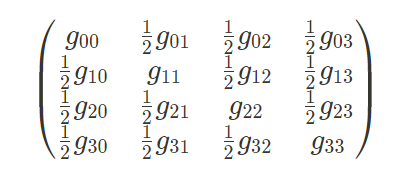
ただし、

$g_{ij} = g_{ji}$

この行列要素を含む和として最初の式を書き直すと、次のようになります。

$ds^2=g_{00}dt^2+g_{01}dt dx+g_{02}dt dy+g_{03}dt dz+g_{11} dx^2+g_{12}dx dy + g_{13}dx dz + g_{22} dy^2+g_{23}dy dz+g_{33} dz^2 \\ = \displaystyle\sum_i \sum_j g_{ij} dx_i dx_j$

ただし、

$dt \equiv dx_0, \quad dx \equiv dx_1, \quad dy \equiv dx_2, \quad dz \equiv dx_3$

ベクトルと行列の積として書く場合は、次のように表現します。

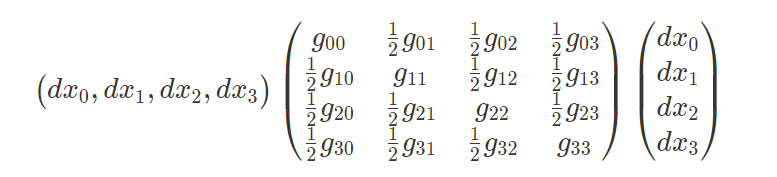
しかし、慣例では、単にΣを省略して書くことが多いです。（アインシュタインの縮約）

$\displaystyle\sum_i \sum_j g_{ij} dx_i dx_j \equiv g_{ij} dx_i dx_j$

ここからが本題です。このgが時空の関数であって変化する場合、曲がった時空の計量であるといいます。

$g_{ij}(\vec{x}) dx_i dx_j$

弦理論の数式4（計量の偏微分）

$\displaystyle\frac{\partial g_{ij}}{\partial x^k} (\vec{x})$

曲がった時空の計量gは、時空間で偏微分ができます。

この偏微分をする場合、分母のxは反変形式（添字が肩の上に乗った形式）で書くのが通例です。

4次元時空では、i,j,kがそれぞれ4通りあるので、4^3=64通りの偏微分係数が存在します。

自明な例

円筒座標(t, r, θ, z)においてgの成分は

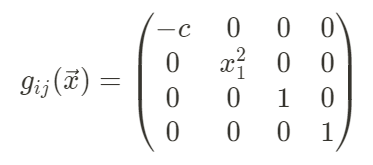
なので、

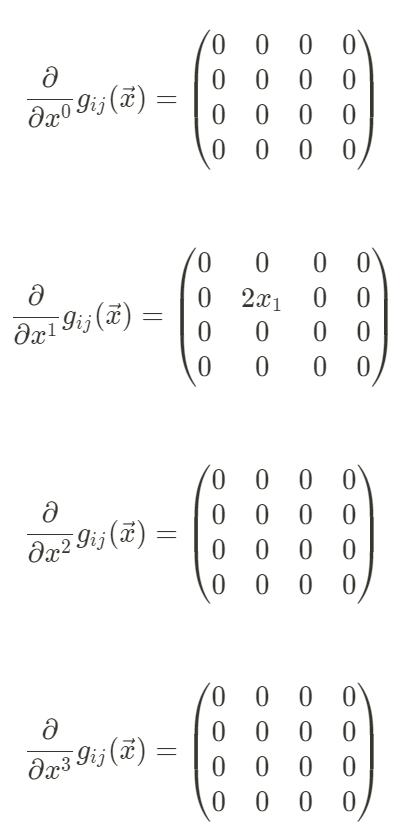
の、64個です。

社会人向け素粒子講座の話